 Cześć! Pisałem tydzień temu sprawdzian z matematyki i dostałem 1, ale chciałbym go poprawić
i prosiłbym o rozwiązanie i WYTŁUMACZENIE jak to zrobiliście.
1. Posługując się przybliżonymi wartościami funkcji trygonometrycznych, wyznacz pozostałe boki
(z dokładnością do 0,01) i kąty w trójkącie prostokątnym mając dane (oznaczenia standardowe)
a= 3, α=32*
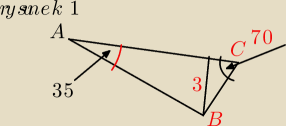
2. oblicz obwód trójkąta ABC z dokładnością do 0,1 (pokazane na rysunku 1)
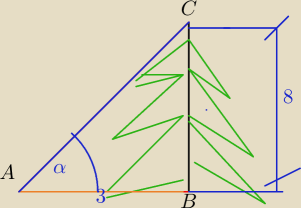
3. Drzewo o wysokości 8m rzuca na ziemię cień długości 3m. pod jakim kątem padają promienie
słoneczne.
4. Na samym brzegu rzeki znajdują się punkty obserwacyjne A i B, a na drugim brzegu, tuż przy
wodzie, znajduje się drzewo D. Wykonano następujące pomiary: |AB| =a oraz |<DAB|=α
i |<DBA| = β. Oblicz szerokość rzeki
D
−−−−−−−−−−−−−−−−−−−−−−−−−|−−−−−−−−−−−−−−−−−−−−−−−−
−−−−−−−−−−−|−−−−−−−−−−−−−−−−−−−−−−−|−−−−−−−−−−−−−−−−
A B
5. Oblicz wysokość h trójkąta korzystając z danych na rysunku jeżeli jego obwód wynosi
36 + 6 √3. Skorzystaj z funkcji trygonometrycznych
Ten rysunek będzie w odpowiedzi do tego posta
Cześć! Pisałem tydzień temu sprawdzian z matematyki i dostałem 1, ale chciałbym go poprawić
i prosiłbym o rozwiązanie i WYTŁUMACZENIE jak to zrobiliście.
1. Posługując się przybliżonymi wartościami funkcji trygonometrycznych, wyznacz pozostałe boki
(z dokładnością do 0,01) i kąty w trójkącie prostokątnym mając dane (oznaczenia standardowe)
a= 3, α=32*
2. oblicz obwód trójkąta ABC z dokładnością do 0,1 (pokazane na rysunku 1)
3. Drzewo o wysokości 8m rzuca na ziemię cień długości 3m. pod jakim kątem padają promienie
słoneczne.
4. Na samym brzegu rzeki znajdują się punkty obserwacyjne A i B, a na drugim brzegu, tuż przy
wodzie, znajduje się drzewo D. Wykonano następujące pomiary: |AB| =a oraz |<DAB|=α
i |<DBA| = β. Oblicz szerokość rzeki
D
−−−−−−−−−−−−−−−−−−−−−−−−−|−−−−−−−−−−−−−−−−−−−−−−−−
−−−−−−−−−−−|−−−−−−−−−−−−−−−−−−−−−−−|−−−−−−−−−−−−−−−−
A B
5. Oblicz wysokość h trójkąta korzystając z danych na rysunku jeżeli jego obwód wynosi
36 + 6 √3. Skorzystaj z funkcji trygonometrycznych
Ten rysunek będzie w odpowiedzi do tego posta
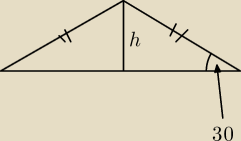 Do zadania 5
Do zadania 5
| BC | 8 | 2 | ||||
Tgα= | = | =2 | ≈69o | |||
| AB | 3 | 3 |
| 2 | ||
.........= 2 | ⇒α≈69o | |
| 3 |
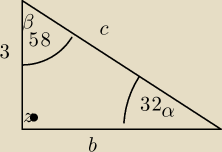 zadanie nr 1
W trojkacie prostokatnym suma dwoch katow ostrych wynosi 90o
skoro jeden ma 32 to drugi ma 58 o ( to powinno byc logiczne
teraz boki
zadanie nr 1
W trojkacie prostokatnym suma dwoch katow ostrych wynosi 90o
skoro jeden ma 32 to drugi ma 58 o ( to powinno byc logiczne
teraz boki
| a | a | 3 | |||
= sin32o ⇒c= | = | = To sobie policz | |||
| c | sin32o | 0,5299 |
| b | ||
np tak | = cos 32o masz juz policzone c cos 32o znajdz w tablicach lub kalkulatorze | |
| c |

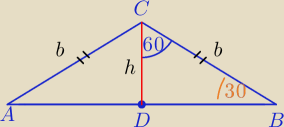 |AB|=a, |AC|=|BC|=b
(*) a+2b=36 + 6 √3
ΔABC− Δrównoramienny
1) W ΔCDB:
|AB|=a, |AC|=|BC|=b
(*) a+2b=36 + 6 √3
ΔABC− Δrównoramienny
1) W ΔCDB:
| 0.5a | √3 | 0.5a | ||||
cos30o= | ⇔ | = | ||||
| b | 2 | b |
| h | ||
sin30= | ||
| b |
| 1 | h | ||
= | |||
| 2 | 6*(9−4√3) |
| 1 | ||
h= | b | |
| 2 |
 Wczoraj nie było Cię na forum?
Zrobisz (4) ?
Wczoraj nie było Cię na forum?
Zrobisz (4) ?
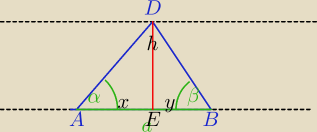 1) W ΔAED:
1) W ΔAED:
| h | ||
tgα= | ⇔h=x*tgα | |
| x |
| h | ||
tgβ= | ⇔h=y*tgβ | |
| y |
| a*tgβ | ||
x= | ||
| tgα+tgβ |
| a*tgβ | ||
h=x*tgα= | *tgα | |
| tgα+tgβ |
| a*tgα*tgβ | ||
h= | ||
| tgα+tgβ |
