Dane są dwa okręgi przecinające się w punkach A i B
siemanko: Dane są dwa okręgi przecinające się w punkach A i B. Jednocześnie te dwa okręgi są styczne do
pewnej prostej w punktach C i D. Udowodnij, że prosta AB przechodzi przez środek odcinka CD.
Jakieś wskazówki?

25 lut 21:15
Eta:
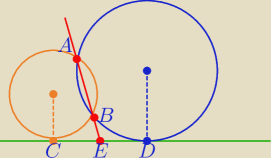
Dwa razy twierdzenie o stycznej i siecznej:
|CE|
2= |AE|*|BE| i |ED|
2=|AE|*|BE|
zatem |CE|=|ED|
wniosek ..... E jest środkiem odcinka CD
c.n.u
25 lut 21:45
Eta:
I co? "siemanko"... pasuje ?
25 lut 23:30
siemanko: Tak, bardzo dziękuję

26 lut 18:07
Eta:

26 lut 18:42

 Dwa razy twierdzenie o stycznej i siecznej:
|CE|2= |AE|*|BE| i |ED|2=|AE|*|BE|
zatem |CE|=|ED|
wniosek ..... E jest środkiem odcinka CD
c.n.u
Dwa razy twierdzenie o stycznej i siecznej:
|CE|2= |AE|*|BE| i |ED|2=|AE|*|BE|
zatem |CE|=|ED|
wniosek ..... E jest środkiem odcinka CD
c.n.u

