| Ix2−xI+1 | |
=1 | |
| Ix+1I−x2 |
 x=0
x=0


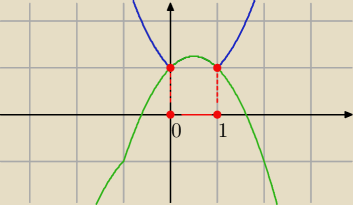
 Wszystkie z przedziału <0, 1>
Wszystkie z przedziału <0, 1>
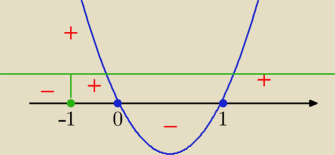 dla x∊(−∞,−1)
x2−x+1=−x−1−x2 ⇒ 2x2+2=0 −−− brak rozw
dla x∊<−1,0> U <1,∞)
x2−x+1=x+1−x2 ⇒ 2x2−2x=0 x=0 lub x=1
dla x∊(0,1) ⇒ −x2+x+1= x+1−x2 ⇒ 0=0 tożsamość ⇒ x∊(0,1)
odp: suma rozwiązań czyli x∊<0,1>
==========
dla x∊(−∞,−1)
x2−x+1=−x−1−x2 ⇒ 2x2+2=0 −−− brak rozw
dla x∊<−1,0> U <1,∞)
x2−x+1=x+1−x2 ⇒ 2x2−2x=0 x=0 lub x=1
dla x∊(0,1) ⇒ −x2+x+1= x+1−x2 ⇒ 0=0 tożsamość ⇒ x∊(0,1)
odp: suma rozwiązań czyli x∊<0,1>
==========
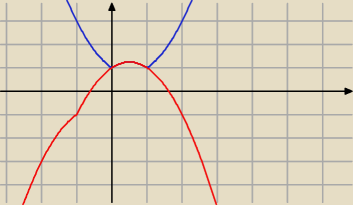
 y=|x2−x|+1
y= |x+1|−x2
y=|x2−x|+1
y= |x+1|−x2
 ale dziękuję
ale dziękuję