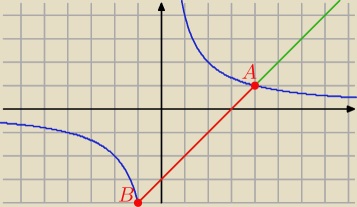
proszę o pomoc i wyjaśnienie Michał99: Poproszę o pomoc : Prosta o równaniu y=a²x+3a przecina hiperbolę o równaniu y=4/x w dwóch punktach A i B. Wyraź długość odcinka AB w zależności od parametru a<0. Wyznacz równanie prostej, która przecina opisaną w zadaniu hiperbolę tak, aby długość odcinka AB była najmniejsza. Zadanie 15 za 7 punktów matura próbna 2018 nowa era rozszerzenie.

Basia: szukamy tych punktów A i B czyli rozwiązaujemy układ równań x≠0

⎧	y=a2x+3a
⎩	y=4/x

4
	= a2x+3a /*x
x

4 = a²x²+3ax a²x+3ax−4=0 a≠0 bo dla a=0 mamy sprzeczność −4=0 mamy mieć dwa punkty wspólne czyli Δ>0 Δ=9a²−4*a²*(−4) = 25a² ponieważ w treści zażądano aby a<0 √Δ = 5|a| = −5a

	−3a+5a		2a		1
x1=		=		=
	2a2		2a2		a

	4
y1=		= 4a
	1   a

	−3a−5a		−8a		−4
x2 =		=		=
	2a2		2a2		a

	4		−4a
y1 =		=		= −a
	−4   a		4

	1
A = (		; 4a)
	a

	−4
B = (		; −a)
	a

|AB| jest najmniesze ⇔ |AB|² jest najmniejsze (bo |AB|>0)

	1		1		1
|AB|2 = (−4−		)2 + (−a−4a)2 = 16 + 2*4*		+		+ 25a2
	a		a		a2

no i szukasz teraz minimum tej funkcji w dziedzinie a∊(−∞;0) wzór funkcji możesz jeszcze przekształacać; zależy jak Ci wygodniej

Eta: 1/ a²x+3a=4/x , x≠0 a²x²+3ax−4=0 Δ= 25a² , √Δ=5a

	1		−4
x=		lub x=
	a		a

to y=4a lub y= −a

	1		−4
A(		,4a) , B(		,−a)
	a		a

	25
|AB|2=		+25a2
	a2

	−50
f'(a)=		+50a
	a3

f^'(a)=0 ......... ⇒ a=1>0 v a=−1 <0 −−− tę przyjmujemy zgodnie z treścią zadania .......................... ........................ uzasadnij ,że to minimum to A(−1,−4) , B(4,1) i |AB|=5√2 prosta ma równanie y=x−3

Basia: Cześć Eto √Δ=−5a bo zażyczono sobie w treści zadania, aby a było ujemne

Eta: Hej Basia Właśnie patrzę,że a<0 Punkty A i B i u mnie i u Ciebie są ok mimo ,że wzięłam √Δ=5a Ty w |AB|² masz coś nie tak ? Sprawdź czy dobrze widzę ...

Michał99: ok przeanalizowałem wszystko i rozumiem! Dzieki wielkie i miłego wieczoru.

Eta:

Eta: @Michał99 Masz może linka do tego arkusza?