Kula Kasia13: Dwie równoległe płaszczyzny przecinają kulę i wyznaczają przekroje o polach 49π cm2 i 4π cm2. Odległość między tymi przekrojami wynosi 9 cm. Oblicz pole powierzchni kuli. Skąd mam wnioskować że przekroje te nie sa po jednej stronie wielkiego koła? Czy ktos mógłby mi to wytłumaczyć?

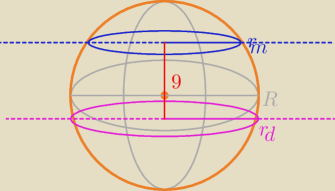
xyz: niebieski przekroj o polu 4π [cm2], gdzie r_m − promien tego przekroju rozowy przekroj o polu 49π [cm2], gdzie r_d − promien tego przekroju zatem 4π = π*r_m² −−> r_m = 2 49π = π*r_d² −−> r_d = 7 P_k = 4*π*R²

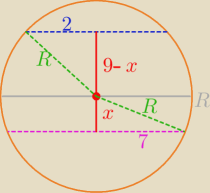
xyz: R² = 2² + (9−x)² R² = 7² + x² −−−−−−−−−−−−−−−−−−−−−−−−− 49 + x² = 4 + (81−18x+x²) ... ... x = 2 zatem R² = 49 + 4 = 53 P_k = 4*π*53 = ...

Kasia13: Dzieki za rozwiazanie 😊 Ale skąd wiedziałeś ze przekroje te nie leżą po jednej stronie?

xyz: Dlaczego nie moga byc po tej samej stronie? drugi promien = 7 skoro odleglosc jest 9 no to ... graficznie tego nie rozrysujesz...

xyz: niestety nie potrafie tego jakos matematycznie uzasadnic moze Mila lub Eta jak sie pojawia to cos napisza.

Eta: Jest ok

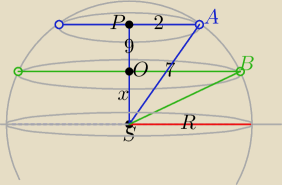
Mila: 1) środek kuli znajduje się między płaszczyznami− to masz rozwiązane. 2) środek kuli jak na rysunku (poniżej płaszczyzn): W ΔAPS: 2²+(9+x)²=R², x>0 W ΔBOS: x²+7²=R² −−−−−−−−−−−− 4+81+18x+x²=x²+49 18x=−36 x=−2∉D