W trójkąt prostokątny ABC o bokach długości |AB|=10, |AC|=8, |BC|=6 wpisano okrą terminator: W trójkąt prostokątny ABC o bokach długości |AB|=10, |AC|=8, |BC|=6 wpisano okrąg o środku w punkcie O. Prosta CO przecina okrag opisany na trójkącie ABC w punkcie D=/=C. Oblicz długość odcinka OD. Prosze o pomoc

Eta: |OD|=2(4−√2) taką masz odpowiedź?

terminator : Niestety nie mam odpowiedzi do tego zadania, czy mógłbym prosić o wskazówki jak do tego dojść?

Eta:

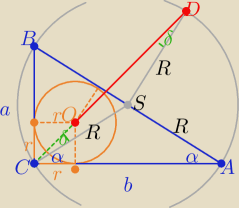
	a+b−c
a=6, b=8, c=10 to R=0,5c=5 i r=		= ..=2
	2

|CO|=r√2=2√2 sinα= 0,6, cosα=0,8 |<ACO|=45^o to |<DCS|=45^o−α to w trójkącie równoramiennym DCS |<DSC|= ...=90^o+2α cos(90^o+2α)= −sin(2α)= −2*0,6*0,8= −0,96 Z twierdzenia cosinusów w ΔDCS: |DC|²= R²+R²+2*R*R*0,96 ⇒ ......... |DC|=7√2 to |OD|= |CD|−|CO|=7√2−2√2= 5√2 ===== Posprawdzaj rachunki .... ( bo poprzednio się pomyliłam

terminator: Bardzo dziękuje, już rozumiem

Eta: Na zdrowie

ja: