Geometria analityczna Kasia:

	1
Wykaż, ze styczna do paraboli o rownaniu y=(		)2−x−2, ktora jest równoległa do cięciwy
	2

AB, gdzie A (0,−2) i B (4,2), ogranicza wraz z osiami ukladu współrzędnych trójkąt o polu równym 8. Wyliczylam pochodną i dalej nie wiem co mam zrobić

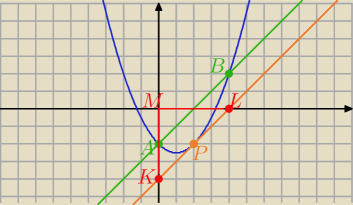
Eta: AB: y= x−2 , a_AB=1 to f^'(x_o)=a_AB= 1 i styczna ma równanie y= f^'(x_o)(x−x_o)+y_o , P(x_o,y_o) −− punkt styczności f^'(x)=x−1 ⇒ x_o= 2 to y_o= f(2)= −2 P(2, −2) styczna ma równanie ........................ y= x−4 P(KLM)= ....... = 8 c.n.w

Eta: Co Cię tak zamurowało?

Eta: No i jeszcze "zjadłaś" w treści x²

Kasia: Szczerze sama nie wiem mam jeszcze pytanie, czemu y0 wyliczamy juz od normalnej funkcji, a nie pochodnej?

Jerzy: Bo wzór na styczną, to: y = f'(x₀)*(x − x₀) + f(x₀)

Kasia: Dziękuje bardzo za pomoc