Proszę o pomoc. Nadii: FUNKCJA Czy znajdzie się jakaś dobra duszyczka która narysuje mi funkcję f(x)=x³−3x²+2? Tylko tak że opisze co robi po kolei (z wyliczaniem ekstremów itd)?

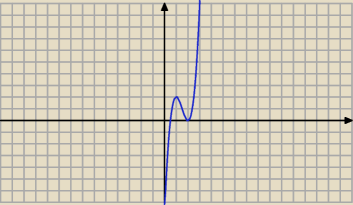
Jerzy: Zacznij od dziedziny, potem policz pochodną.Poszukamy ekstremów lokalnych.

Nadii: Jak policzyć pochodną?

Jerzy: f'(x) = 3x² − 6x Teraz znajdź miejsca zerowe pochodnej.

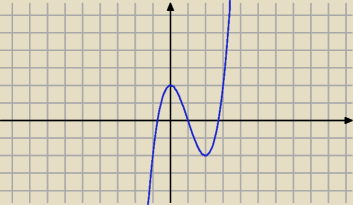
Jerzy: Tutaj jest poprawny wykres,ten wyżej nie.

Nadii: Miejsca zerowe pochodnej to 0 i 2

Jerzy: Dobrze. Czy pochodna zmienia znak w tych punktach ?

Nadii: nie?

Jerzy: Jak to nie ...naszkicuj sobie na kartce wykres pochodnej.

Nadii: Echhhh

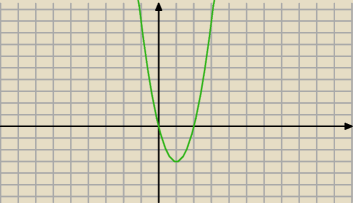
Jerzy: To jest wykres pochodnej..czy w ounktach x = 0 oraz x = 2 zmienia znak ?

Nadii: tak

Jerzy: Jak zmienia ?

Nadii: Przepraszam dopiero teraz wrociłam. x³−3x²+2 Pochodna: 3x²−6x 3x²−6x=0 3x(x−2)=0 x=0 x=2 W(0)=2 W(2)=−2 I wówczas mogę juz narysować tę funkcję prawda? I teraz mam pytanie Dalsza część polecenia to korzystając z wykresu tej funkcji znaleźć zależność liczby k pierwiastków równania x³−3x²+2=m od wartości parametru m i narysować wykres funkcji k=k(m) i zbadać jej ciągłość. Mam po prostu sobie ogarnąć cos typu że np. 1 rozw. dla m∊(−∞,−2)∪(2,+∞), 2 rozw. dla m∊{−2,2}, 3 rozw. dla m∊(−2,2) I dla tego narysować wykres funkcji k=k(m) która kazdej wartości parametru przyporzadkuje liczbe rozw tego równania?

Nadii: Pewnie źle co nie?

Nadii: Przypominam się

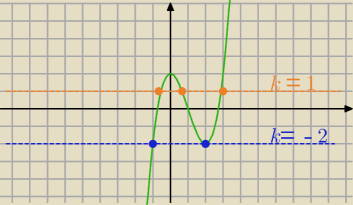
iteRacj@: wartoćci funkcji k(m) to wnioski z tego rysunku wypisałaś je dobrze o 17:23 narysuj osobno tej funkcji wykres będzie widać czy jest ciągła

Nadii: W sensie jaki wykres? Ten o którym wspomniałam na koncu? A i do czego jest ten wykres wyzej i daczego na nim jest zaznaczone np k=1?

iteRacj@: nie po polsku napisałam miało być: narysuj osobno wykres funkcji k=k(m) która każdej wartości parametru m przyporządkowuje liczbę rozwiązań tego równania − na osi odciętych wartości m − na osi rzędnych ilość rozwiązań

iteRacj@: k=1 jest tylko przykładowo

Nadii: Ok, dziękuję

iteRacj@: a narysowałaś ? i wiesz dlaczego jest nieciągła?

Nadii: Narysowałam. Mozesz wyjaśnić

iteRacj@: nie ma co pisać, to widać, masz dwa punkty nieciągłości −2 i 2

Nadii: Aaaaa czyli wystarczy napisać ze funkcja nie jest ciągła bo ma te dwa punkty nieciaglosci?

iteRacj@: funkcja nie jest ciągła w całej dziedzinie, bo ma dwa punkty nieciągłości, (w pozostałych punktach jest ciągła)