Wyznacz najmniejsza i największą wartość funkcji f(x)=U{2x}{1+x^2} dla x∊<-2,2>
yakamoz: | | 2x | |
Wyznacz najmniejsza i największą wartość funkcji f(x)= |
| dla x∊<−2,2> |
| | 1+x2 | |
| | x3−4x2+x | |
1. licze pochodną f'(x)= |
| |
| | (1+x2)2 | |
2. przyrównuje do zera i mam x=0 oraz x=1
| | 4 | |
później wychodzi mi ze najmniejsza wartość to y=− |
| dla x=−2 a największa y=1 dla x=1 |
| | 5 | |
Mam dobre wyniki ?
25 lut 11:31
piotr: ((2 x)/(1 + x2))' = −(2 (x2 − 1))/(1 + x2)2
f(−1)min = −1
f(1)max = 1
25 lut 11:47
Eta:
ok
25 lut 11:49
Eta:
ok ma piotr
25 lut 11:49
Eta:
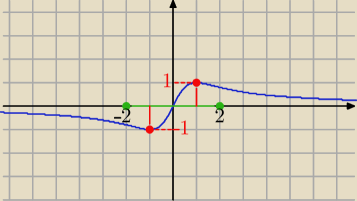
25 lut 11:52
PW:
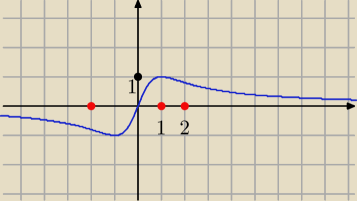
Funkcja jest nieparzysta, wystarczy ją zbadać na przedziale <0,2>. f(0)=0, zaś dla x∊(0, 2>
Jak wiadomo dla x>0 jest
przy czym równość ma miejsce tylko dla x=1. Wynika stąd, że
| | 2 | | 2 | |
|
| = f(x)≤ |
| =1, x∊(0, 2> |
| | | | 2 | |
Z nieparzystości automatycznie wynika, że dla (−x)∊<−2,0)
f(−x)=−f(x)≥−1,
przy czym równość ma miejsce dla (−x)=2, czyli x=−2.
25 lut 11:54
PW: Nie widziałem wypowiedzi szanownych przedmówców, ale za to podałem rozwiązanie bez użycia
pochodnej.
25 lut 11:56
PW: Korekta.
przy czym równość ma miejsce dla (−x)=1, czyli x=−1.
Często mylą mi się sąsiednie klawisze, przepraszam. Rysunek jest dobry, widać tę nieparzystość.
25 lut 12:04
Eta:
To jeszcze taki sposób ( też bez pochodnej

1+x
2>0
to y(1+x
2)=2x ⇒yx
2−2x+y=0
Δ≥0 ⇒4−4y
2 ≥0 ⇒ y∊<−1,1>
ZW
f=<−1,1>
<−1,1> ⊂<−2,2>
to f(−1)=−1 −− minimum
f(1)=1 −−− maximum
25 lut 12:05
PW: Piękny

. Zawsze sposób elementarny jest lepszy od tego stosującego zaawansowany
aparat, mam taką prywatną opinię.
25 lut 12:18
Eta:

25 lut 12:31

 Funkcja jest nieparzysta, wystarczy ją zbadać na przedziale <0,2>. f(0)=0, zaś dla x∊(0, 2>
Funkcja jest nieparzysta, wystarczy ją zbadać na przedziale <0,2>. f(0)=0, zaś dla x∊(0, 2>
 1+x2>0
to y(1+x2)=2x ⇒yx2−2x+y=0
Δ≥0 ⇒4−4y2 ≥0 ⇒ y∊<−1,1>
ZWf=<−1,1>
<−1,1> ⊂<−2,2>
to f(−1)=−1 −− minimum
f(1)=1 −−− maximum
1+x2>0
to y(1+x2)=2x ⇒yx2−2x+y=0
Δ≥0 ⇒4−4y2 ≥0 ⇒ y∊<−1,1>
ZWf=<−1,1>
<−1,1> ⊂<−2,2>
to f(−1)=−1 −− minimum
f(1)=1 −−− maximum
 . Zawsze sposób elementarny jest lepszy od tego stosującego zaawansowany
aparat, mam taką prywatną opinię.
. Zawsze sposób elementarny jest lepszy od tego stosującego zaawansowany
aparat, mam taką prywatną opinię.
