funkcja homograficzna 00000:

	ax+b
Dziedziną f. homograficznej f(x)=		jest zbiór R−{−1}. Miej. zer. funkcji to
	x+c

	3
−		, a do jej
	2

	−1
wykresu należy punkt A (		, −8).
	2

a)oblicz wart. a,b,c i narysuj wykres

	ax+b
b)zbadaj liczbę rozwiązań równania |		|=m ze wzg. na wart. parametru m, m∊R
	x+c

Mam a) a=−4 b=−6 c=1 Tylko nie mam pojęcia jak zabrać się za b) czy mógłby mi ktoś wytłumaczyć?

iteRacj@: dokończ polecenie i narysuj najpierw wykres f(x), a potem |f(x)|, wtedy będzie można zbadać liczbę rozwiązań równania ze względu na wartość parametru m

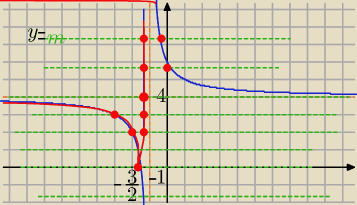
Eta: dla a= −4, b= −6, c= 1

	−4x−6
f(x)=
	x+1

	−4x−6		4x+6		2
Równanie |		|=m ⇔ |		|= |4+		|=m
	x+1		x+1		x+1

	2
Rysujesz wykres f(x)= 4+
	x+1

to |f(x)| −−− odbijasz tę część wykresu f(x) spod osi Ox nad oś Ox czerwony wykres Teraz "tniemy ten wykres prostymi y=m Równanie ma 0 rozwiązań dla m<0 1 rozwiązanie dla m=0 lub m=4 2 rozwiązania dla m ∊(0, 4) U (4,∞)

Eta: Z niebieskiej części "uciekł" mi przy rysowaniu czerwony kolorek

00000: Dziękuję

Eta: Na zdrowie ....