Geometria xy: Dwa okręgi przecinają się w dwóch punktach. Z jednego z tegoż tych punków poprowadzono średnice obu okręgów. Następnie połączono odcinkiem drugie końce tych średnic. Wykaż że odcinek ten przechodzi przez drugi punkt przecięcia okręgów.

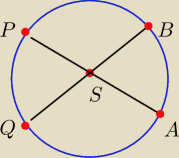
PW: Rysunek trochę nieudany. P i Q − punkty wspólne okręgów, S − środek. Czy może QABP jest prostokątem?

xy: Tak, ale co mi to daje?

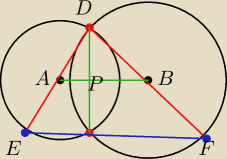
Basia: jakie są wzgledem siebie trójkaty ADB i EDF ? jaki jest odc.PD względem AB? z odpowiedzi na te pytania wynika odpowiedź

xy: Jeśli P to ten drugi punkt przecięcia: AB łączy środki ramion trójkąta DEF, czyli jest równoległe do EF. Kąt DPF jest oparty na średnicy, czyli DP jest prostopadłe do AB?

Basia: DPF jest oparty na średnicy, ale nie jest kątem wpisanym w okrąg przecież P nie leży na okregu niemniej jednak DR jest ⊥ AB (R drugi czerwony punkt) wynika to z tego, ze RADB jest deltoidem a P punketm przecięcia jego przekatnych

Basia: przepraszam źle zrozumiałam u mnie P to przecięcie tych dwóch zielonych u Ciebie druga czerwona kropka i wtedy oczywiście jest tak jak piszesz

PW: Tak, ale co ci to daje

Basia: jak to co? EP⊥AP i FP⊥AP ⇒ EP||FP czyli P∊odc.EF

PW: Basiu, ja nie do Ciebie.

Basia: a to przepraszam PW

xy: Dzięki