wykresy funkcji 00000:

	|x|+1
Jak to narysować? F(x)=
	|x|−1

	|x|+1		2
Przekształcam		=1+
	|x|−1		|x|−1

2		2		2
	−−−−		−−−−		+1
x		|x|		|x|−1

pierwsze 2 przekształcenia wychodzą dobrze, przy 3 jest źle, te przeształcenia powinny być dobrze, bo jak je wpisuje w kalkulatorze graficznym wychodzi tak jak jest w odp. Czy mógłby mi ktoś wytłumaczyć jak nalezy zrobić ten przykład?

Timor i pumba:

	x+1
Rysujesz dla |x|≥0 czyli y=
	x−1

Potem masz lustrzane odbicie wzgledm osi OY bo to jest funkcja typu f(|x|)

00000:

	2		2
Nie rozumiem. Co muszę narysować, żeby przejść z		do		+1?
	|x|		|x|−1

iteRacj@: nie zaczynaj od rysowania wykresu funkcji z wartością bezwzględną narysuj tak jak napisał Timor i pumba

	2
możesz tamten wzór przekształcić do postaci f(x)= 1+
	x−1

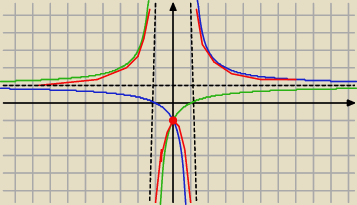
Eta: Założenia : x≠±1

	x+1
dla x≥0 i x≠1 to y=		−−− pierwsza część hiperboli
	x−1

	−x+1
dla x<0 i x≠ −1 to y=		−−−− druga część hiperboli
	−x−1

	|x|+1
Obydwie części to wykres f(x)=
	|x|−1

Eta:

	x+1		x−1+2		2
y=		=		= 1+		,
	x−1		x−1		x−1

	−x+1		−2
y=		= −1+
	−x−1		x+1

00000: o Boże. Skąd sie bierze ta część wspólna?

Eta: 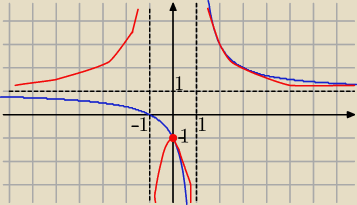2 sposób

	x+1
Umiesz narysować wykres f(x)=
	x−1

	|x|+1
to f(|x|)=
	|x|−1

powstaje przez symetrię względem osi Oy tej części wykresu f(x) która znajduje się tylko po prawej stronie na lewą stronę

	|x|+1
Obydwie te części to wykres f(|x|) =
	|x|−1

00000: Czy w tym drugim (zielonym) y nie pownno być bez minusa przy 1? (15:58)

Eta: tak +1

00000: Już nie ważne, łapię drugim sposobem. Dziękuję bardzo

Eta:

00000:

	|x|
Czy mógłby mi ktoś jeszcze wytłumaczyć jak narysować taką funkcję: f(x)=		kiedy moduł
	x−1

jest tylko na jednym x?

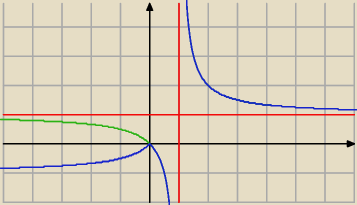
Basia: najlepiej oddzielnie dla x≥0 i x<0

	x		x−1+1		1
dla x≥0 rysujesz		=		= 1+
	x−1		x−1		x−1

	1
czyli kolejno		i przesunięcie o wektor u→=[1;1]
	x

wymazujesz to co Ci zostało po lewej stronie osi OY do wymazania jest to zielone i poczekaj z tym wymazywaniem

	−x		x		x−1+1		1
dla x<0 rysujesz		= −		= −		= −[ 1 +		]
	x−1		x−1		x−1		x−1

czyli praktycznie to co przedtem miałeś wymazać odbijasz symetrycznie względem OX

00000: Dziękuję bardzo