dowod jak to narysowac jack: Nie potrafię tego narysować, żeby ruszyć dalej. Wiem, że A, A₁, A₂⊂Ω oraz A₁∩A₂⊂A. Wykaz ze P(A)≥P(A₁)+P(A₂)−1

Benny: P(A₁∪A₂)=P(A₁)+P(A₂)−P(A₁∩A₂) 1≥P(A₁)+P(A₂)−P(A₁∩A₂) P(A₁∩B₂)≥P(A₁)+P(A₂)−1 P(A)≥P(A₁∩A₂)≥P(A₁)+P(A₂)−1

jack: tyle to mam w rozwiązaniach w książęce mnie interesuje rysunek bo nie umiem sobie tego wyobrazić

iteRacj@: 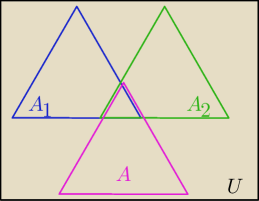A, A₁, A₂⊂Ω A₁∩A₂⊂A

iteRacj@: P(A)=P(A₁)+P(A₂)−1 jedyna ilustracja równości, jaka mi przychodzi do głowy to sytuacja A=A₁=A₂=Ω czy są jakieś inne?

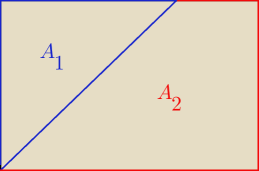
Basia: są; np. A₁∪A₂ = Ω i A=A₁∩A₂=0

iteRacj@: dzięki muszę ćwiczyć wyobraźnię

jack: Basiu nie bardzo rozumiem , a gdzie w taki razie będzie A. Powiem że widziałem to tak jak w tych trojkatach twój rysunek ...? gdzie o czym w takim razie jest A?

Pytający: Basi chodziło raczej o zbiór pusty, A=A₁∩A₂=∅, |A|=|A₁∩A₂|=0, w tym przypadku na rysunku tegoż A nie dostrzeżesz. Jednak to tylko jeden z przypadków, gdy zachodzi równość, o którą spytała Iteracj@.