potrzebuję pomocy WojteK: Trójkąt równoramienny o podstawie 16 i ramionach 17 podzielono odcinkiem równoległym do podstawy na dwie figury o równych polach. Oblicz wysokość powstałego trapezu.

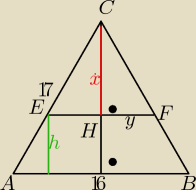
justka: ΔABC jest podobny do Δ EFC

x		H		x		15		8
	=		⇒		=		⇒ y =		x
y		8		y		8		15

H² = 17² − 8² H = 15

	1
PABC =		*16*15 = 120
	2

	1
PEFC =		*PABC = 60
	2

P_EFC =0,5* x*2y

	8
60= x*		*x
	15

	15√2
x =
	2

h = H − x

	30 −15√2
h =
	2

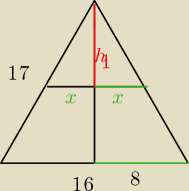Godzio: h² + 8² = 17² h = 15

h		h1
	=
8		x

2x*h1		2x+16
	=		* (h−h1)
2		2

15x = 8h₁

	15x
h1 =
	8

2xh₁ = (2x+16)(15−h₁) 2xh₁ = 30x −2xh₁ + 240 − 16h₁ 4xh₁ = 30x +240 − 16h₁

	15x		15x
4x *		= 30x + 240 − 16*
	8		8

7,5x² = 30x + 240 − 30x 7,5x2 = 240 x²=32 x=4√2

	15x
h1 =		= 7,5√2
	8

	8√2 + 16
P =		* 7,5√2
	2

P = (4√2 + 8) * 7,5√2 = 56 + 60√2 = 4(14 + 15√2)

Godzio: ale namodziłęm h₂ = h−h₁ = 15 − 7,5√2 a do Pola którego nie trzeba było liczyć wsadziłem wysokość trójkąta ale do h₁ jest dobrze