Jest dana funkcja f
dodalemnowezadanie:
Funkcja f dana jest wzorem f(x)=(x−2p)
2+p gdzie p ∊ R. Wyznacz zbior wartosci funkcji g oraz
podaj rownanie osi symetrii jej wykresu.
g(x)=f(p−x)
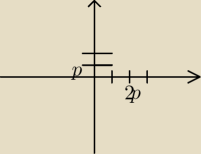
Zrobilem przykladowy rysunek jak moze wygladac funkcja f(x),nie umiem rysowac paraboli tutaj
wiec niech p to 1 jednostka w kartezjanskim ukladzie.Wierzcholek(2p,p) wspolczynnik a dodatni.
Po przeksztalceniu:
g(x)=(p−x−2p)
2+p=−(x+p)
2+p.
Nie zgadza sie z odpowiedziami.Odpowiedz to zw:<p;
∞),x=−p
22 lut 17:08
the foxi:
f(x)
f(p) − przesuwamy wykres o p w lewo, wierzchołek (p,p)
f(−x) − symetria względem osi OY, więc po "sklejeniu" z poprzednią zamianą mamy wierzchołek w
punkcie (−p,p)
Teraz chyba jasne

Albo inaczej
Tu masz błąd: (−x−p)
2≠−(x+p)
2
(−x−p)
2=(−x−p)(−x−p)=(x+p)(x+p)=(x+p)
2
Stąd g(x)=(x+p)
2+p
22 lut 17:17
the foxi:
Korekta, w drugiej linijce powinno być: f(x+p)
22 lut 17:18
Janek191:
g(x) = f( p − x) = ( p − x − 2p)2 + p = ( − x − p)2 + p = ( x − p)2 + p
ZWg = < p, +∞)
22 lut 17:19
dodalemnowezadanie: Ehh no racja,dziekuje
22 lut 17:21
 Funkcja f dana jest wzorem f(x)=(x−2p)2+p gdzie p ∊ R. Wyznacz zbior wartosci funkcji g oraz
podaj rownanie osi symetrii jej wykresu.
g(x)=f(p−x)
Zrobilem przykladowy rysunek jak moze wygladac funkcja f(x),nie umiem rysowac paraboli tutaj
wiec niech p to 1 jednostka w kartezjanskim ukladzie.Wierzcholek(2p,p) wspolczynnik a dodatni.
Po przeksztalceniu:
g(x)=(p−x−2p)2+p=−(x+p)2+p.
Nie zgadza sie z odpowiedziami.Odpowiedz to zw:<p;∞),x=−p
Funkcja f dana jest wzorem f(x)=(x−2p)2+p gdzie p ∊ R. Wyznacz zbior wartosci funkcji g oraz
podaj rownanie osi symetrii jej wykresu.
g(x)=f(p−x)
Zrobilem przykladowy rysunek jak moze wygladac funkcja f(x),nie umiem rysowac paraboli tutaj
wiec niech p to 1 jednostka w kartezjanskim ukladzie.Wierzcholek(2p,p) wspolczynnik a dodatni.
Po przeksztalceniu:
g(x)=(p−x−2p)2+p=−(x+p)2+p.
Nie zgadza sie z odpowiedziami.Odpowiedz to zw:<p;∞),x=−p
 Albo inaczej
Tu masz błąd: (−x−p)2≠−(x+p)2
(−x−p)2=(−x−p)(−x−p)=(x+p)(x+p)=(x+p)2
Stąd g(x)=(x+p)2+p
Albo inaczej
Tu masz błąd: (−x−p)2≠−(x+p)2
(−x−p)2=(−x−p)(−x−p)=(x+p)(x+p)=(x+p)2
Stąd g(x)=(x+p)2+p