nierówność Klaudia: jak rązwiązać tą nierówność : m³−4m²−4m+48>0 ?

Klaudia: Pomoże ktoś Please

PW: Uczyłaś się o wzorach Cardano?

Eta: Jeżeli to zadanie ze szkoły średniej? to sprawdź czy wszystko dobrze przepisałaś ? Jeżeli ze studiów ... to skorzystaj ze wskazówki PW

Eta: Klaudia ....zaniemówiłaś ? "Please"

PW: A, to odpuścimy. Ja i tak tych wzorów nie pamiętam

adam: −3 jest pierwiastkiem

dar: Po co wzory Cardano? Poszukaj dzielnikow liczby 48

Adamm: −3 nie jest pierwiastkiem

adam: pochodna to 3m²−8m−4

PW: A całka to

	1		4
		x4−		m3−2m2+48m+C, C∊R.
	4		3

adam: i co z tego?

PW: A co z tego, że pochodna to...?

adam: można ekstrema wyliczyć

adam: a z całki nic

Adamm: z całki można wyliczyć pole pod wykresem

PW: Co mają ekstrema do miejsc zerowych? A całka i owszem − gdyby umiał bez pochodnej znaleźć, gdzie ma ekstremum, to...

Klaudia: Całek nie znam. wydaje mi się, że to jako nierówność wielomianowa, ale szukałam pieriastkówi nie mogę znaleźć, a −3 też nie jest pierwiastkiem

Klaudia: Tu mam treść zadania i swoje rozwiązanie: https://www.dropbox.com/s/j947y3zz1j4chlm/20180222_100511.jpg?dl=0

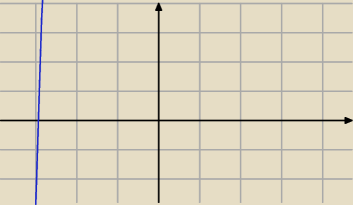
PW: Z tą całką to był żart − przekomarzanie się ze złymi pomysłami adama. Jeżeli się nie uczyłaś o wzorach Cardano, to nie rozwiążesz tej nierówności. Posługując się pochodną możesz znaleźć ekstrema, co przekona o istnieniu tylko jednego pierwiastka wielomianu. Można różnymi metodami szukać przybliżenia tego pierwiastka. Na przykład: w(−3)=−27−36+12+48<0 − pierwiastek jest nieco większy od (−3) (patrz rysunek, na którym widać tylko fragmencik wykresu, bo wielomian jest dobrany złośliwie, nie zmieści się w tej skali zbyt wiele). w(−2,9)=−24,389−33,64+11,6+48=1,571>0 Szukany pierwiastek jest więc w przedziale (−3, −2,9). Dla mało wybrednych mamy więc przybliżone rozwiązanie: w(m)>0 dla m≥−2,9, w(m)<0 dla m≤−3. Liczba m, dla której w(m)=0 jest do dokładnego obliczenia paskudnymi wzorami Cardano.

PW: No tak, wzięłaś ze środka swojego rozwiązania zupełnie innego zadania jakąś nierówność i kazałaś ją rozwiązywać dla wszystkich m, co jest w tamtym zadaniu zbędne. Podstawowa zasada na forum: PODAJ DOKŁADNĄ TREŚĆ ZADANIA (a nie swoje sugestie czy domysły). Nie chce mi się z tobą gadać.

aniabb: m>4

Klaudia: Ale wiem o co chodzi w zadaniu, doprowadziłam rozwiązywanie do tej postaci nierówności i chyba o to w tym chodzi. Mam natomiast problem z jej rozwiązaniem, aby uzyskany wynik połączyć z dziedziną. Nie potrafię tego zrobić i dlatego szukam pomocy na forum.

sxl: Ahh, może po kolei. 1. Wyznaczasz dziedzinę 2. Szukasz dzielników wyrazu wolnego 3. Zapisujesz w najprostszej postaci 4. Rozwiązania zaznaczasz na osi liczbowej 5. Rysujesz krzywą przechodzącą przez pierwiastki (jeśli pierwiastek jest podwójny, poczwórny itd to krzywa odbija, a jeśli nie to przechodzi dalej) 6. Zaznaczasz na osi liczbowej takimi kreseczkami te obszary, które spełniają założenia zadania, tzn. w twoim przypadku są większe od 0 −−−> wszystko co będzie nad osią liczbową 7. Sprawdzasz czy dziedzina wyklucza Ci jakieś rozwiązania − jeśli tak to je odrzucasz, jeśli nie zapisujesz przedział, który jest Twoją odpowiedzią do zadania

sxl: Skoro masz nierówności wielomianowe to zapewne równania wielomianowe już miałaś, zatem myślę, że sobie poradzisz. Powodzenia.

aniabb: ponieważ jest trochę wredny ten przykład i nic nie możesz znaleźć zauważasz szukając, że dla wszystkich sprawdzanych dodatnich podzielników reszty są dodanie a dopiero od −3 są ujemne więc podejrzewasz że pierwiastek jest około −3 a ponieważ Twoja dziedzina zaczyna się od 4 to np. liczysz pochodną i okazuje się że w tym przedziale cały czas rośnie więc spełnia warunki a z kolei dla ujemnych cały czas maleje więc nie zawróci do zera

Benny: Źle rozpisana suma sześcianów. Powinno być (x₁+x₂)((x₁+x₂)²−3x₁x₂) I nierówność m³−4m²−12m+48>0 (m−4)(m−2√3)(m+2√3)>0

Klaudia: Ahhhh.... dzięki wielkie Benny, taki błąd a tyle zamieszania

Mariusz: "Jeżeli się nie uczyłaś o wzorach Cardano, to nie rozwiążesz tej nierówności" Otóż tutaj PW kłamie bo wszystko co potrzebne było jeszcze niedawno w liceum Przydadzą się : schemat Hornera (można go zastąpić podstawieniem) wzory skróconego mnożenia wzory Vieta równanie kwadratowe Twierdzenie Bezouta trygonometria Gdybyśmy mogli używać zespolonych to twierdzenie Bezouta można by zastąpić pierwiastkami z jedynki a do trygonometrii doszlibyśmy ze wzoru de Moivre m³−4m²−4m+48>0 Można rozwiązać sposobami znanymi licealiście m³−4m²−4m+48=0 Zastosujmy schemat Hornera aby uzyskać sumę potęg dwumianu (x−a) 1 −4 −4 48 4/3 1 −8/3 −68/9 1024/27 4/3 1 −4/3 −28/3 4/3 1 0 4/3 1

	4		28		4		1024
(m−		)3−		(m−		)+		=0
	3		3		3		27

	4
y=m−
	3

	28		1024
y3−		y+		=0
	3		27

y=u+v

	28		1024
(u+v)3−		(u+v)+		=0
	3		27

	28		1024
u3+3u2v+3uv2+v3−		(u+v)+		=0
	3		27

	1024		28
u3+v3+		+3u2v+3uv2−		(u+v)=0
	27		3

	1024		28
u3+v3+		+3(u+v)(uv−		)=0
	27		9

	1024
u3+v3+		=0
	27

	28
3(u+v)(uv−		)=0
	9

	1024
u3+v3=−
	27

	28
uv=
	9

	1024
u3+v3=−
	27

	21952
u3v3=
	729

	1024		21952
t2+		t+		=0
	27		729

	512		240192
(t+		)2−		=0
	27		729

	512−√240192		512+√240192
(t+		)(t+		)=0
	27		27

	1
u3=		(−512−√240192)
	27

	1
v3=		(−512+√240192)
	27

	1
y=		(3√−512−√240192+3√−512+√240192)
	3

	4		1
m−		=		(3√−512−√240192+3√−512+√240192)
	3		3

	1
m=		(3√−512−√240192+3√−512+√240192+4)
	3

Aby sprawdzić czy to jedyny pierwiastek równania dzielisz wielomian przez dwumian Licealista powinien sobie poradzić z równaniem (nierównością) wielomianowym trzeciego stopnia

Timor i pumba: A świstak i td ...

Klaudia: Wow

Mariusz: Powyższy sposób działa także dla równań czwartego stopnia W przypadku równań czwartego stopnia oprócz powyższego sposobu działa też pomysł z rozłożeniem wielomianu na iloczyn dwóch trójmianów kwadratowych Jeśli chodzi o rozkład wielomianu czwartego stopnia na iloczyn dwóch trójmianów kwadratowych to sposób z zapisaniem trójmianów kwadratowych w postaci ogólnej z użyciem współczynników nieoznaczonych, wymnożeniem tych trójmianów kwadratowych , porównaniem współczynników i zapisaniem w postaci układu równań może wymagać więcej obliczeń niż sposób z rozkładem najpierw na różnicę kwadratów Zamiast współczynników nieoznaczonych używasz wtedy wzorów skróconego mnożenia oraz wyróżnika trójmianu kwadratowego Licealista powinien sobie poradzić także z równaniem czwartego stopnia wykorzystując pomysł z rozkładem wielomianu czwartego stopnia na iloczyn dwóch trójmianów kwadratowych Równanie czwartego stopnia prowadzi na ogół do równania trzeciego stopnia bądź równania szóstego stopnia sprowadzalnego do równania trzeciego stopnia

PW: Już nie będę kłamał. Rzeczywiście maturzysta powinien sobie z tym poradzić.

Mariusz: PW śledzisz program liceum ? schemat Hornera (można go zastąpić podstawieniem ) wzory skróconego mnożenia wzory Vieta równanie kwadratowe Twierdzenie Bezouta trygonometria (np wzór na sinusa i cosinusa sumy) Przydałyby się jakieś wiadomości o funkcjach aby zdefiniować sobie funkcje odwrotną do trygonometrycznej Jeśli chodzi o równanie czwartego stopnia to aby je sprowadzić do równania trzeciego stopnia to wystarczą wzory skróconego mnożenia i wyróżnik trójmianu kwadratowego Użycie trygonometrii powinno sprawić że liczby zespolone nie będą potrzebne a tych liczb nie ma w liceum

Maciess: Pytanie do pana Mariusza. Czy metoda której pan używa do równań 3 stopnia to to samo co na tej stonie? http://www.kowalskimateusz.pl/rozwiazywania-rownan-wielomianowych/ Pierwszy raz się spotykam z taką metodą rozwiązywania, a w żadnym swoim podręczniku jej nie mam, więc nie wiem czy jest to w programie. Chyba, że mam jakąś gorszą szkołe

Krzysiek60: Tak Mozesz sobie o niej poczytac w ksiazce Algebra wyzsza W Sierpinki lub Mostwowski Elelmty algebry wyzszsej .

iteRacj@: @Mariusz CKE podaje, że w maju 2017 17,25% tych, którzy do egzaminu maturalnego przystąpili, nie zdało matematyki. Żeby zdawać musieli być do matury dopuszczeni czyli znać cały materiał szkoły średniej, a mimo to nie zdołali na podstawie uzyskać 30% punktów. Ci na pewno nie poradziliby sobie z "równaniem czwartego stopnia, wykorzystując pomysł z rozkładem wielomianu czwartego stopnia na iloczyn dwóch trójmianów kwadratowych bądź równaniem szóstego stopnia sprowadzalnego do równania trzeciego stopnia". A pozostali czy by sobie poradzili i czy chcieliby korzystać z rozwiązań, które podajesz (np. wpis z 24 lut 2018 05:03)? Mam wątpliwości...