Pomocy abla: Podstawa AB trójkąta równoramiennego ABC zawarta jest w prostej x + y + 1 = 0. Ramię BC zawiera się w prostej 2x − y − 1 = 0. Wyznacz równanie prostej k zawierającej ramię AC wiedząc, że punkt P = (−4, 0) należy do prostej k. Obliczyłam na razie punkt B (0, −1) jak zabrać się dalej za to zadanie?

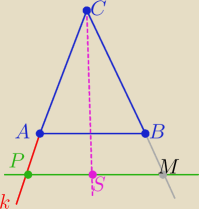
Eta: 1/ AB: y= −x−1 Prosta PM ∥AB i P(−4,0) PM: y=−(x+4) ⇒ y=−x−4 2/ rozwiązujemy układ równań BC i PM otrzymując M( −1,−3) to środek S odcinka PM : S( −5/2, −3/2) 3/ Prosta CS ⊥ PM CS: y=(x+5/2)−(3/2) ⇒ y= x+1 4/ rozwiązując układ równań prostych CS i BC otrzymasz .... C( 2,3) zatem prosta k=PC =AC

	−3
aPC =		=1/2
	−6

to k: y=1/2(x−x_C)+y_C k: y= 1/2x+2 w postaci ogólnej k: x−2y+4=0 ==========

Eta: Wstań rano i przepisz !( skoro od ponad 3 godzin nie interesujesz się tym zadaniem