okręgi
Agata: Wyznacz te wartosci parametru m meR dla których okregi
o1: (x−3)2 + (y−m)2 − 2 oraz o2 : x2 +y2 − 2mx −6y +9 −m2 =0
są styczne wewnętrznie
20 lut 20:31
Jerzy:
A jaki jest warunek, aby tak było ?
20 lut 20:32
Janek191:
Popraw równanie okręgu o1
20 lut 20:33
Agata: Jerzy |S1S2| =|R−r|
20 lut 22:03
Agata: Janek191 tak mam zapisane
20 lut 22:05
Basia: a widzisz tam jakies rownanie ?
w rownaniu musi byc znak =
20 lut 22:06
Agata: (x−3)2 + (y−m)2 − 2 =0
21 lut 06:56
Agata: 
21 lut 19:07
Agata: Może ktos pomoc mi wykonać cało to zadanie?
21 lut 19:09
21 lut 19:18
Krzysiek60: To dziewczyna nie maluje paznocki ?
21 lut 21:59
manicurzystka:
To zamiast życzliwie sprawdzić zadanie, ogladasz paznokcie?
21 lut 23:02
Mila:
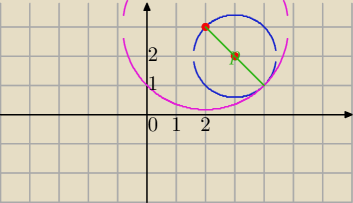
o1: (x−3)
2 + (y−m)
2 = 2
o2 : x
2 +y
2 − 2mx −6y +9 −m
2 =0 ⇔
(x−m)
2−m
2+(y−3)
2−9+9−m
2=0
(x−m)
2+(y−3)
2=2m
2
S
1=(3,m), r
1=
√2
S
2=(m,3) r
2=
√2*m i m>0
√(3−m)2+(m−3)2=|
√2−
√2*m| ⇔
√2*(m−3)2=|
√2*(1−m)|
√2*|m−3|=
√2*|1−m|
|m−3|=|m−1| i m>0
m
2−6m+9=m
2−2m+1
−4m=−8
m=2
====
21 lut 23:55
Mila:
Panowie zawsze oceniają kobietę po wdziękach, tacy już są.
21 lut 23:56
iteRacj@:
Nie, to nieprawda. Przecież wszyscy deklarują, że liczy się charakter a nie uroda.
22 lut 07:14
aniabb: z układem limbicznym nie wygrasz
22 lut 10:53
iteRacj@:
święta racja
22 lut 23:19
