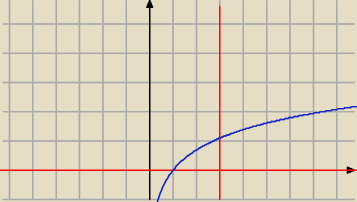
sd sda: pole obszaru y=lnx y=0 x=√8 mam pole narysowane i pisze całke do liczenia pola górna granica √8 dolna 1 ∫lnx=1/√8−ln1=√2/2−0

sda: ale cos robie zle '/

Jerzy: A jaką masz całkę: ∫lnxdx ?

sda: tak

sda: ale w odp mam ze pole wychodzi 3√2ln2−√8+1

Jerzy: Co "tak" ? ∫lnxdx = ?

sda: ja tam pochodna zrobiłem xD ALE NIC mi to nie daje i tak nwm jak wyliczyc

sda: całke mam ∫lnxdx

Jerzy: Liczysz przez części: v' = 1 u = lnx

	1
v = x u' =
	x

Basia: P = ₁∫^√8lnx dx I=∫ln(x) dx =

	1
[ u=lnx u'=		]
	x

[v'=1 v=x] I = x*ln(x) − ∫1dx = x*ln(x)−x +C = x(ln(x) − 1) + C P = √8*(ln√8−1) − 1*(ln1−1) = √8*(ln√8−1) −1(0−1) = 2√2*(ln(2√2) − 1)+1

	3
mozna jeszsze zapisac ln(2√2) = ln23/2 =		*ln(2)
	2

i bedzie

	3
P = 2√2*		*ln2 − 2√2 + 1 = 3√2*ln(2) − 2√2+1
	2

sda: no to mam lnx²−ln|x|

Jerzy: Brawo Basiu ... jestem pod wrażeniem.

Basia:

Jerzy: Masz już "gotowca" wyżej, więc przepisz bezwiednie do kajetu i nie myśl o tym, skąd co sie wzięło.

sda: ja to nie mam na zadanie tylko musze nauczyc sie tego na kolosa xD

Jerzy: O to mi chodziło, więc tym bardziej próbuj sam, a my Ci pomożemy. Problem w tym, abyś to zrozumiał.