paramtr A/rozwiąz nierówność
Michał :
Dobry wieczór, potrzebuję pomocy/rady/rozwiązania nierówności, gdyby ktoś mógł pomoc będę
wdzięczny:
√x−5>=11−x
x−5>=0 <−D(f)
x>5 <−Dziedzina
√x−5−11+x>=0
√x−5+x−5−6>=0
t=
√x−5
t+t
2−6>=0
Δ=25
t
1=−3
t
2=2
√x−5<= −3 |
2 √x−5>=2 |
2
|x−5|<=9 |x−5|>=4
x−5<=9 v x−5 >= −9 x−5>=4 v x−5 <= −4
x<=14 v x>=−4 x>=9 v x<=1
x∊<−4;14> x∊(−
∞;−1>u<9;+
∞)
Suma przedziałów : <9;14> // odp w książce <9;+oo)
I od razu podłączam pod post zadanie 2:
Odczytaj z wykresu w zależności od parametru a liczbę rozwiązań.
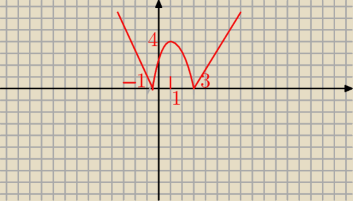
f(x)=2|(x+1)(x−3)|
| | −16 | |
f(x)=2|x2−2x−3| => Δ=16 => q= |
| =−4 |
| | 4 | |
Rysuje mam miejsca zerowe, wyliczyłem wierzchołek paraboli, ponieważ wartość bezwględna to
odbiłem to coś pod osią OX na drugą stronę. Pytanie według odp parametr a przyjmuje 2 rozw.
dla 0 i (8;+oo) co znaczy ze wierzchołek funkcji musi być w punkcie 8 (chyba). Czemu? Ta
dwójka przed nawaisem ma jakiś wpływ na wierzchołek?
Wydaje mi się że ta 2 mówi mi o tym pod jakim kątem (większym czy mniejszym) parabolama ramiona
względem osi. Eh słabo to w słowa ubrałem bo nie potrafię tego wytłumaczyć.
No to proszę o rozwiązania/pomoc z wytłumaczeniem, gdyby ktoś miał czas i chęci będę wdzięczny!

pozdrawiam cieplutko Michał <3
19 lut 19:43
Michał : Chyba w zadaniu 2 już wiem czemu q=8 (po przekształceniu) 2f(x) <−− zwiększy hmmnn wysokość (oś
Y) dwa razy.
Jezeli się nie mylę proszę o potwierdzenie =)
19 lut 20:12
ford:
Co do zad. 1 z nierównością − poległeś przy rozwiązywaniu
√x−5<= −3
 √x−5
√x−5 to liczba dodatnia
−3 to liczba ujemna
nierówność przyjmuje zatem postać:
liczba dodatnia <= liczba ujemna, a to jest sprzeczność, dlatego
√x−5<= −3 w ogóle nie
rozwiązujesz tylko piszesz że to sprzeczność
Co do zad. 2 − tak, ta dwójka przed nawiasem ma wpływ na wierzchołek, wykres jest 2 razy
bardziej rozciągnięty w górę, w szczególności − ta "górka" którą przedstawiłeś na wykresie,
będzie 2 razy wyższa

19 lut 20:15
PW: Pomysł, że x−5=p{x−5)2 bardzo dobry, ale dalej...
Niestworzone rzeczy wypisujesz, np.
(*) √x−5≤−3
i wniosek
|x−5|≤9.
Przecież (*) jest zdaniem fałszywym dla wszystkich x z dziedziny − co tu dalej rozwiązywać?
..............................................................................
Rozwiążmy "normalnie".
(1) √x−5≥11−x
Dziedziną równania jest przedział <5,∞) z uwagi na definicję pierwiastka.
Łatwo zauważyć, że jeżeli 11−x<0, to (1) jest zdaniem prawdziwym (lewa strona nieujemna, prawa
ujemna). Wobec tego wszystkie x∊(11,∞) są rozwiązaniami.
Weźmy dalej x≤11 i należące do dziedziny, czyli x∊<5, 11>. Dla takich x obie strony są
nieujemne, po podniesieniu obu stron nierówności do kwadratu dostajemy więc równorzędną
nierówność
(√x−5)2≥(11−x)2, x∊<5, 11>.
x−5≥121−22x+x2
x2−23x+126≤0
(x−9)(x−14)≤0
x∊<9, 14>∩<5, 11>
x∊<<9, 11>.
|Odpowiedź: Rozwiązaniami nierówności są x∊<<9, 11>∪(11,∞)=<9,∞).
19 lut 20:20
Michał : @Ford Dziękuję Ford

Rozumiem gdzie leży mój błąd. Mam pytanie, gdy mam np.
√coś <= liczba
ujemna to jest zawsze sprzeczność?
@PW te niestworzone rzeczy już rozumiem czemu, są niestworzone. Racja to straszna głupota była
z mojej strony. Mam pytanie do 11−x<=0 czyli x>=11 bo teraz wiem ze od (11;+
∞) prawa strona
równania jest ujemna, a to co po lewej jest dodatnie (mowie o
√x−5), czy to się nie powinno
wykluczy? Tak samo x<=11 skąd w ogóle pomysł na to żeby x<=11, napisałes "weźmy dalej x<=11
należącje do dziedziny" wziałes to x<=11 bo lewa strona równania to 11−x? Eh, wiem ze moze
zadaje głupie pytania (przepraszam), ale ja tego nie widzę tak po prostu PW

A tak poza tym dzięki chłopaki za pomoc.
19 lut 20:50
PW: Właśnie o to idzie: jeżeli x>11, to prawa strona jest ujemna, a nierówność
√x−5≥liczba ujemna
jest prawdziwa w sposób oczywisty − nie trzeba rozwiązywać, wszystkie x>11 ją spełniają.
19 lut 21:08
Michał : Aaaaa

Okkkkkkkkk rozumiem! GENIALNE!

Dziękuję PW teraz to dostrzegam czemu x>11 spełnia tą nierówność

Czyli potem bierzesz ten zakes <5,11> aby sprawdzić czy w tym zakresie jakieś liczby spełnią
nierówność prawda?
Podnosisz obie strony nierówności do kwardatu i łączysz wyrazy podobne otrzymując:
x
2−23x+126<=0
oki a czy nie powinno się zrobić wartości bezwględnej podnosząc
√x do kwadratu?
19 lut 21:21
ford:
nie, dlatego że po podniesieniu √x do kwadratu otrzymujesz: (√x)2
zaś wzór z wartością bezwzględną to: √x2 = |x|
wbrew pozorom, (√x)2 oraz √x2 to nie jest to samo
wyrażenie (√x)2 jest określone dla x≥0 (liczba podpierwiastkowa nie może być ujemna) bo pod
pierwiastkiem masz sam x
zatem jeśli chcesz dokonywać działań na √x, w szczególności podnosić to do kwadratu, to (po
cichu) zakładasz, że x≥0, stąd nie ma sensu mieszać wartości bezwzględnej, bo wiadomo że x i
tak jest dodatni
zatem (√x)2 = x
wyrażenie √x2 jest określone dla wszystkich x2≥0 (liczba podpierwiastkowa nie może być
ujemna)
ponieważ x2 to liczba dodatnia (lub równa 0 dla x=0), to x2≥0 jest nierównością typu
liczba dodatnia ≥ 0 co zachodzi zawsze
zatem x∊R (ujemne iksy też spełniają założenie, np. √(−3)2 = √9 = 3.
Wzór √x2=|x| wziął się stąd, żeby nie zapewnić dodatniość wyrażeniu √x2, nawet jeśli x
będzie ujemny
bez tego wzoru, czyli √x2 = x otrzymalibyśmy np. dla x=−3 głupotę:
√(−3)2 = −3
wg wzoru:
√(−3)2 = |−3| = 3, co jest prawdą
Pozdrawiam
19 lut 22:17
ford:
*pod koniec pomyłka, miało być:
żeby zapewnić dodatniość wyrażeniu √x2 nawet jeśli x będzie ujemny
19 lut 22:21
Michał :
Ok

dzięki Ford za objaśnienie sprawy, doceniam i jeszcze raz dzięki panowie za pomoc

W
tych zadaniach.
Pozwolę sobie też zadać kolejne pytania odnośnie tematu funkcji kwadratowej (aby nie tworzyć
kolejnych tematów na forum).
Mianowicie mam pytanie co do rys. wykresów funkcji:
−f(x) − odbcie względem OX
f(−x) − odbicie względem OY
|f(x)| − wszystkie wartości ujemne zamieniamy na dodatnie
f(|x|) − 1−szej i 4−tej ćwiartka zostają odbite na miejsce 2−giej i 3−ciej
Teraz pytanie jak to wyglada we wzorach funkcji kwadratowej?
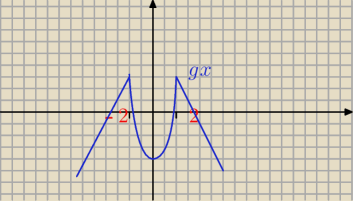
np. −|x
2−4|+2 = g(x)
1.wyliczam Δ=16 miejsca zerowe x
1=−2 x
2=2
2. nakładam wartość bezględną (czyli |f(x)|) //To jak w tym wzorze wyglądaloby f(|x|)?
3. obrót względem osi OX (czyli −f(x)) // To jakby wyglądał w tym wzorze obrót względem osi OY?
4. podnoszę wykres cały o dwie wartości w górę.
Głupio to znowu pisać

ale proszę o pomoc, podanie przykładów w których będzie
pokazane, co jak wygląda

Dziękuję Michał

19 lut 22:43
ford:
2. f(|x|) akurat w tym wzorze nie zrobi żadnej zmiany w stosunku do wykresu f(x)
3. obrót względem osi OY nie zrobi żadnej zmiany w stosunku do wykresu z punktu 2.
20 lut 21:11
 Dobry wieczór, potrzebuję pomocy/rady/rozwiązania nierówności, gdyby ktoś mógł pomoc będę
wdzięczny:
√x−5>=11−x
x−5>=0 <−D(f)
x>5 <−Dziedzina
√x−5−11+x>=0
√x−5+x−5−6>=0
t=√x−5
t+t2−6>=0
Δ=25
t1=−3
t2=2
√x−5<= −3 | 2 √x−5>=2 |2
|x−5|<=9 |x−5|>=4
x−5<=9 v x−5 >= −9 x−5>=4 v x−5 <= −4
x<=14 v x>=−4 x>=9 v x<=1
x∊<−4;14> x∊(−∞;−1>u<9;+∞)
Suma przedziałów : <9;14> // odp w książce <9;+oo)
I od razu podłączam pod post zadanie 2:
Odczytaj z wykresu w zależności od parametru a liczbę rozwiązań.
f(x)=2|(x+1)(x−3)|
Dobry wieczór, potrzebuję pomocy/rady/rozwiązania nierówności, gdyby ktoś mógł pomoc będę
wdzięczny:
√x−5>=11−x
x−5>=0 <−D(f)
x>5 <−Dziedzina
√x−5−11+x>=0
√x−5+x−5−6>=0
t=√x−5
t+t2−6>=0
Δ=25
t1=−3
t2=2
√x−5<= −3 | 2 √x−5>=2 |2
|x−5|<=9 |x−5|>=4
x−5<=9 v x−5 >= −9 x−5>=4 v x−5 <= −4
x<=14 v x>=−4 x>=9 v x<=1
x∊<−4;14> x∊(−∞;−1>u<9;+∞)
Suma przedziałów : <9;14> // odp w książce <9;+oo)
I od razu podłączam pod post zadanie 2:
Odczytaj z wykresu w zależności od parametru a liczbę rozwiązań.
f(x)=2|(x+1)(x−3)|
 pozdrawiam cieplutko Michał <3
pozdrawiam cieplutko Michał <3
 √x−5 to liczba dodatnia
−3 to liczba ujemna
nierówność przyjmuje zatem postać:
liczba dodatnia <= liczba ujemna, a to jest sprzeczność, dlatego √x−5<= −3 w ogóle nie
rozwiązujesz tylko piszesz że to sprzeczność
Co do zad. 2 − tak, ta dwójka przed nawiasem ma wpływ na wierzchołek, wykres jest 2 razy
bardziej rozciągnięty w górę, w szczególności − ta "górka" którą przedstawiłeś na wykresie,
będzie 2 razy wyższa
√x−5 to liczba dodatnia
−3 to liczba ujemna
nierówność przyjmuje zatem postać:
liczba dodatnia <= liczba ujemna, a to jest sprzeczność, dlatego √x−5<= −3 w ogóle nie
rozwiązujesz tylko piszesz że to sprzeczność
Co do zad. 2 − tak, ta dwójka przed nawiasem ma wpływ na wierzchołek, wykres jest 2 razy
bardziej rozciągnięty w górę, w szczególności − ta "górka" którą przedstawiłeś na wykresie,
będzie 2 razy wyższa 
 Rozumiem gdzie leży mój błąd. Mam pytanie, gdy mam np. √coś <= liczba
ujemna to jest zawsze sprzeczność?
@PW te niestworzone rzeczy już rozumiem czemu, są niestworzone. Racja to straszna głupota była
z mojej strony. Mam pytanie do 11−x<=0 czyli x>=11 bo teraz wiem ze od (11;+∞) prawa strona
równania jest ujemna, a to co po lewej jest dodatnie (mowie o √x−5), czy to się nie powinno
wykluczy? Tak samo x<=11 skąd w ogóle pomysł na to żeby x<=11, napisałes "weźmy dalej x<=11
należącje do dziedziny" wziałes to x<=11 bo lewa strona równania to 11−x? Eh, wiem ze moze
zadaje głupie pytania (przepraszam), ale ja tego nie widzę tak po prostu PW
Rozumiem gdzie leży mój błąd. Mam pytanie, gdy mam np. √coś <= liczba
ujemna to jest zawsze sprzeczność?
@PW te niestworzone rzeczy już rozumiem czemu, są niestworzone. Racja to straszna głupota była
z mojej strony. Mam pytanie do 11−x<=0 czyli x>=11 bo teraz wiem ze od (11;+∞) prawa strona
równania jest ujemna, a to co po lewej jest dodatnie (mowie o √x−5), czy to się nie powinno
wykluczy? Tak samo x<=11 skąd w ogóle pomysł na to żeby x<=11, napisałes "weźmy dalej x<=11
należącje do dziedziny" wziałes to x<=11 bo lewa strona równania to 11−x? Eh, wiem ze moze
zadaje głupie pytania (przepraszam), ale ja tego nie widzę tak po prostu PW  A tak poza tym dzięki chłopaki za pomoc.
A tak poza tym dzięki chłopaki za pomoc.
 Okkkkkkkkk rozumiem! GENIALNE!
Okkkkkkkkk rozumiem! GENIALNE!  Dziękuję PW teraz to dostrzegam czemu x>11 spełnia tą nierówność
Dziękuję PW teraz to dostrzegam czemu x>11 spełnia tą nierówność  Czyli potem bierzesz ten zakes <5,11> aby sprawdzić czy w tym zakresie jakieś liczby spełnią
nierówność prawda?
Podnosisz obie strony nierówności do kwardatu i łączysz wyrazy podobne otrzymując:
x2−23x+126<=0
oki a czy nie powinno się zrobić wartości bezwględnej podnosząc √x do kwadratu?
Czyli potem bierzesz ten zakes <5,11> aby sprawdzić czy w tym zakresie jakieś liczby spełnią
nierówność prawda?
Podnosisz obie strony nierówności do kwardatu i łączysz wyrazy podobne otrzymując:
x2−23x+126<=0
oki a czy nie powinno się zrobić wartości bezwględnej podnosząc √x do kwadratu?
 Ok
Ok  dzięki Ford za objaśnienie sprawy, doceniam i jeszcze raz dzięki panowie za pomoc
dzięki Ford za objaśnienie sprawy, doceniam i jeszcze raz dzięki panowie za pomoc  W
tych zadaniach.
Pozwolę sobie też zadać kolejne pytania odnośnie tematu funkcji kwadratowej (aby nie tworzyć
kolejnych tematów na forum).
Mianowicie mam pytanie co do rys. wykresów funkcji:
−f(x) − odbcie względem OX
f(−x) − odbicie względem OY
|f(x)| − wszystkie wartości ujemne zamieniamy na dodatnie
f(|x|) − 1−szej i 4−tej ćwiartka zostają odbite na miejsce 2−giej i 3−ciej
Teraz pytanie jak to wyglada we wzorach funkcji kwadratowej?
np. −|x2−4|+2 = g(x)
1.wyliczam Δ=16 miejsca zerowe x1=−2 x2=2
2. nakładam wartość bezględną (czyli |f(x)|) //To jak w tym wzorze wyglądaloby f(|x|)?
3. obrót względem osi OX (czyli −f(x)) // To jakby wyglądał w tym wzorze obrót względem osi OY?
4. podnoszę wykres cały o dwie wartości w górę.
Głupio to znowu pisać
W
tych zadaniach.
Pozwolę sobie też zadać kolejne pytania odnośnie tematu funkcji kwadratowej (aby nie tworzyć
kolejnych tematów na forum).
Mianowicie mam pytanie co do rys. wykresów funkcji:
−f(x) − odbcie względem OX
f(−x) − odbicie względem OY
|f(x)| − wszystkie wartości ujemne zamieniamy na dodatnie
f(|x|) − 1−szej i 4−tej ćwiartka zostają odbite na miejsce 2−giej i 3−ciej
Teraz pytanie jak to wyglada we wzorach funkcji kwadratowej?
np. −|x2−4|+2 = g(x)
1.wyliczam Δ=16 miejsca zerowe x1=−2 x2=2
2. nakładam wartość bezględną (czyli |f(x)|) //To jak w tym wzorze wyglądaloby f(|x|)?
3. obrót względem osi OX (czyli −f(x)) // To jakby wyglądał w tym wzorze obrót względem osi OY?
4. podnoszę wykres cały o dwie wartości w górę.
Głupio to znowu pisać  ale proszę o pomoc, podanie przykładów w których będzie
pokazane, co jak wygląda
ale proszę o pomoc, podanie przykładów w których będzie
pokazane, co jak wygląda  Dziękuję Michał
Dziękuję Michał 