Całkowanie, pole figury ograniczonej krzywymi nieogarniety: Witam, niestety z powodu choroby opuściłem zajęcia dotyczące całek, przez co uczę się samodzielnie korzystając z materiałów, ale nie jestem pewny wyniku jednej całki, jak też nie wiem jak obliczyć pole figury ograniczonej krzywymi. zad nr 1. obliczyć z twierdzenia o całkowaniu przez części ∫x sin 4x dx = ? Nie wiem czy dobrze, ale wynik wyszedł mi −1/4cos(4x) + c ? ___________________________________________________ zad nr 2. Obliczyć pole figury ograniczonej krzywymi: y= −x² +3x +3; y = −1; Proszę o pomoc i ew. przykład rozwiązania. Dziękuję i pozdrawiam.

Mila: wynik możesz sprawdzić obliczając pochodną

	1		1
(−		cos4x)'=−		*(−sin(4x))*4=sin4x nie otrzymano funkcji podcałkowej.
	4		4

= 1) ∫xsin4x dx−..

	1
[x=u, dx=du, dv=sin4x dx, v=∫sin4x dx=−		cos4x]
	4

	1		1
cd..=x*(−		) cos4x+		∫cos4xdx=
	4		4

	1		1
=−		x*cos(4x)+		sin(4x) +C
	4		16

PW: Pochodna funkcji

	1
−		cos(4x)+C
	4

jest równa sin(4x), a więc całka wyznaczona źle − pochodna powinna być równa xsin(4x).

nieogarniety: Witam, czy w tej sytuacji byliby Państwo w stanie sprawdzić poprawność zadań? Dziękuję ślicznie za wytłumaczenie zadania nr 1. Przykład rozwiązań w linku w postaci PDF http://docdro.id/bxAlzkk Pozdrawiam.

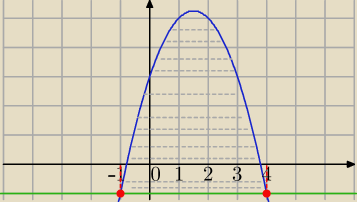
Mila: Dobrze. zad nr 2. Obliczyć pole figury ograniczonej krzywymi: y= −x² +3x +3; y = −1; Granice całkowania : punkty przecięcia krzywych −x²+3x+3=−1 −x²+3x+4=0 Δ=9+16=25

	−3−5		−3+5
x=		= lub x=		=−1
	−2		−2

−1≤x≤4

	1		1
P=∫−14(−x2+3x+4) dx=[−		x3+3*		x2+4x] −14=
	3		2

	1		3		1		3
=−		*43+		*42+4*4−(−		*(−1)3+		−4)=
	3		2		3		2

	125
=
	6

nieogarniety: Czyli rozumiem, że z załącznika zadania poprawnie rozwiązałem? Dziękuję za analizę. Pozdrawiam i życzę miłego wieczoru!

Mila: Wzajemnie, owocnej pracy