z QWERTY:

	4		f(x+1)
Dana jest funkcja f(x)=2−		. Rozwiąż nierówność		>0
	x		f(x−1)

QWERTY: Jakieś podpowiedzi

Benny:

	4
f(x+1)=2−
	x+1

	4
f(x−1)=2−
	x−1

QWERTY:

	12
Naszkicuj wykres funkcji f(x)=		−3.Wyznacz wartość parametru m dla których równanie
	|x|+2

f(x)=m² ma dwa rozwiązania.

	12		|x|		12		v[−2,−3]		12
f(x)=				>f(x)=				> f(x)=		−3
	x				|x|				|x|+2

nie wiem co dalej

Benny: Najpierw przesuwasz o [−2,−3] dopiero później moduł.

QWERTY: zrobi ktoś to

Eta:

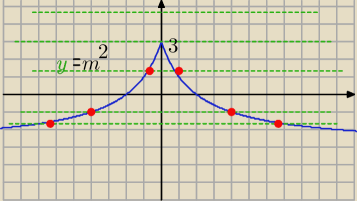
	12
y=		−3 −−− rysujesz wykres
	|x|+2

y=m² Dwa rozwiązania są dla m²<3 ⇒ m(−√3,√3)

QWERTY: jak to narysowałaś

Eta:

	12
dla x≥0 f(x)=		−3
	x+2

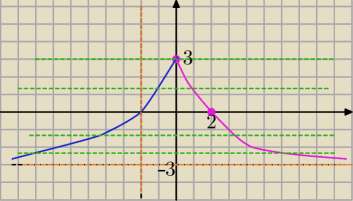
i odbijasz tę część symetrycznie względem osi Oy otrzymując y= U{12}{|x|+2|−3 m²<3 i m²> −3 to m²<3 ⇒ m∊ ...........

Eta:

	12
.....otrzymując y=		−3
	|x|+2

Eta: https://matematykaszkolna.pl/strona/167.html gałąź hiperboli dla x≥0