geometria jack: Dwa boki trójkąta wpisanego w okrąg, o promieniu R są długosci R√3 i 0,5R. Jaką długosc ma trzeci bok. Proszę o pomoc.

jack: nikt nic nie wie

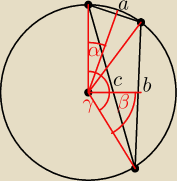
g: c² = 2R²*(1−cos γ) cos γ = cos(2α+2β) = .... (staram się to wyrazić pry pomocy sin α i sin β które są znane) = (1−2sin²α)(1−2sin²β) − 3sin α sin β √(1−sin²α)(1−sin²β) sin α = 1/4, sin β = √3/2

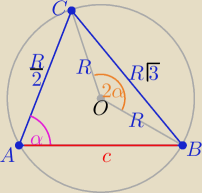
Eta: 1/ z twierdzenia cosinusów w ΔBOC

	R2+R2−3R2
cos(2α)=		= .... −1/2
	2R*R

to 2α=120^o więc α=60^o i z twierdzenia cosinusów w ΔABC (R√3)²=(R/2)²+c²−2*c*(R/2)*cos60^o ....................................... 4c²−2Rc−11R²=0 Δ= 180R² , √Δ=6√5R

	2R±6√5R
c=
	8

	1±3√5
c=		R
	4

==================

jack: WIELKIE THANKS !