Funkcja liniowa pike: Funkcja liniowa Odczytaj miejsca zerowe, jej przedzialy monotocznicznosci oraz zbior rozwiazan nie rownosci. { 2x+4 dla x ∊ (−∞; −1> f(x) = { −x+1 dla x ∊ (−1;4> {−3 dla x ∊ (4;∞) Powie mi ktos jak cos takiego rozwiazac?

iteRacj@: przyrównujesz do zera 2x+4, sprawdzasz, czy wynik należy od przedziału (−∞; −1> jesli należy to masz pierwsze miejsce zerowe tak samo dla −x+1 dla −3 nie sprawdzasz, bo nie jest równe zero

pike: i to jest znalezienie zbioru rozwiazan nierownosci? co z miejscem zerowym i przedzialami?

pike: aa dobra. nie doczytalem. a co z reszta?

iteRacj@: tak jak napisałam: masz pierwsze miejsce zerowe jest to szukanie miejsc zerowych

iteRacj@: y=2x+4 y=−x+1 y=−3 są to funkcje liniowe po współczynnikach kierunkowych poznajesz czy są rosnące, malejące czy stałe takie są oczywiście w przedziałach podanych przy ich wzorach i juz masz monotoniczność

iteRacj@: zbioru rozwiązań nierównosci nie da sie okreslić, bo nie jest podana żadna nierówność może czegoś nie dopisałeś...

pike: dobra, dzieki pomoglas bardzo

iteRacj@: to się cieszę

pike: No tak, nie dopisalem ze "zbior rozwiazan nierownosci dla f(x) ≥ −3

pike: Pomoze ktos?

pike: .

iteRacj@: szukamy zbioru rozwiazań nierównosci f(x) ≥ −3, zasada taka sama jak przy szukaniu miejsc zerowych tej funkcji rozwiązujesz nierówność 2x+4≥−3 sprawdzasz, czy wynik należy od przedziału (−∞; −1> lub znajdujesz część wspólną wyniku i przedziału tak samo dla −x+1 dla −3 widać, że jest prawdziwe dla wszystkich x ∊ (4;∞)

Krzysiek60: 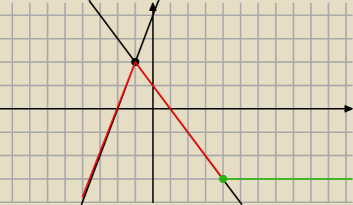pike \Ty jestes w miare leń bo nawet nie chce sie tobie zrobic wykresu Odczytuje miejsca zerowe \ x=−2 x=1 monotonicznosc rosnie x∊(−∞ −1) maleje x∊ (−1,4) stala x∊ (4 ∞)