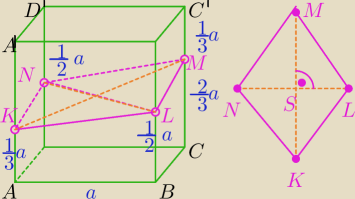
Stereometria Kasia13: Sześcian ABCDA'B'C'D' o krawędzi a przecięto płaszczyzna przechodzącą przez srodku krawędzi BB' i DD' i dzielącą krawędź AA' w stosunku 1:3 licząc od wierzchołka S. Oblicz pole przekroju . Prosze o pomoc

iteRacj@:

	1		1		1		7
|KL|2=|NM|2=a2+[(		−		)a]2=a2+[(		)a]2=		a2
	2		3		6		6

	2		1		1		7
|NK|2=|LM|2=a2+[(		−		)a]2=a2+[(		)a]2=		a2
	3		2		6		6

|NK|=|KL|=|LM|=|NM| przekrój jest rombem

	1
PKLMN=		*|NL|*|KM|
	2

|NL|=a√2=2|SL| z tw. PItagorasa dla ΔKSL

	7		1
|KS|2=|KL|2−|SL|2=		a2−(		a√2)2
	6		2

	√6
|KS|=		a
	3

	1		√6		√3
więc PKLMN=		*a√2*		a=		a2
	2		3		3

iteRacj@: poprawka |KM|=2*|KS|

	1		2√6		2√3
P KLMN=		*a√2*		a=		a2
	2		3		3