styczna kici: Wyznacz równanie stycznej do wykresu funkcji f(x)= ^1−6x2_6x² przechodzącej przez punkt P(−3,1/2)

Basia: y=ax+b a= f'(−3) i prosta przechodzi przez P

kici: ale ten punkt nie nalezy do wykresu chybai nie wiem czy to mozna tak zrobic

Basia: tam w mianowniku jest 6x² ? w takim razie nie mozna za chwile napisze jak

kici: tak 6x²

Benny: y=ax+b

1
	=−3a+b
2

	1
b=		+3a
	2

	1
y=ax+		+3a
	2

Prosta ma jeden punkt wspólny z funkcją.

	1		1
ax0+		+3a=		−1
	2		6xo2

a=f'(−3)

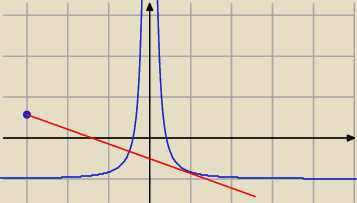
Basia: a≠f'(−3) bo jak napisala Kicia P ∉ wykresu funkcji poza tym to nie jest ani parabola, ani krzywa zamknieta styczna w jednym punkcie moze miec inny punkt wspolny z ta krzywa i tak tu bedzie mniej wiecej tak jak na rysunku

Eta: W/g moich obliczeń styczna ma równanie

	1		1
y= −		x−		w punkcie (1,−5/6)
	3		2

kici: to dobry wynik tylko co zrobic najpierw

kici: jak dojsc do x0

Eta: równanie stycznej y=f^'(x_o)(x−x_o)+y_o i przechodzi przez P(−3,1/2)

	1
f'(x)= −
	3x3

Należy rozwiązać równanie:

1		1		1−6x2
	=−		(−3−x)+
2		3x3		6x2

..................... 3x³+6x²−2x−7=0 w(1)=0 (x−1)(3x²+9x+7)=0

	1−6		5
tylko xo=1 jest rozwiązaniem to yo=		= −
	6		6

i mamy punkt styczności (1, −5/6) dokończ.........

Basia: @Kicia czy tam aby czegos w tresci nie brakuje?

Eta: @ kicia Myślę,że rozumiesz,że opuściłam indeks x_o w tym równaniu ... dla łatwości zapisów

kici: Czemu w nawiasie jest −3−x

Eta: P(−3,1/2) za x podstawiamy −3 a za y 1/2 zostawiamy x_o i y_o otrzymując

1
	=f'(xo)( −3−xo)+yo ( ja nie pisałam tych indeksów xo ...tylko x
2

1		1		1−6x2
	=−		( −3−x)+
2		3x3		6x2

.................. po rozwiazaniu otrzymujemy .... wracam do x_o=1 to y_o=f(x_o)=..=−5/6 punkt styczności (x_o,y_o)=(1,−5/6) i pisz równanie stycznej.... już kumasz ?

Satan: Bo podstawiasz punkt do stycznej. x_o to x, a za x podstawiliśmy −3 z punktu, przez który styczna przechodzi.

Eta:

Basia:

	1
prosta przechodzi przez (−3;		) wiec Eta podstawia
	2

x=−3 i y=1/2 rownoczesnie opuszcza wskaznik przy x₀ formalnie byloby

1		1		1−6x02
	= −		(−3−x0)+
2		3x03		6x02

teraz pomin wskaznik i juz

Eta:

kici: Dziwny ten wzor Korzystając z tego "wyjściowego" y=f(x) − f`(x) * x Wyszło mi prostsze równanie kwadratowe z dwoma pierwiastkami 1/3 i −1/3 Zmylił mnie poprostu ten wzór bo nie ogarnęłam czemu odejmuje cię x Ale wynik wyszedł ten sam Nie trzeba było się bawić z dzieleniem wielomianu Dzięki

kici: Czyli nie trzeba tu podstawiać tej −3? Hmm

MπM: No niby nie ma tego we wzorze więc chyba jest zbedne

MπM: Coś tutaj jest nie tak ...

MπM: Jak możecie podstawić −3 za x skoro we wzorze jest x0 a nie z o to chodzi To x tyczy się wzoru funkcji liniowej y=ax+b a wzóry masz na a i b trzeba to polaczyc w całość

kici: Dziekuje ta pora mi nie służy heh

Eta: Ot masz "babo placek" Rozwiążesz , podasz jak na tacy ...... i jeszcze marudzą ! "dziwny wzór" , "wyszło mi prostsze równanie" .............. Echhhhhhhhhhhh

MπM : Trochę lipa z tym wielomianem w takim zadaniu heh

MπM : Wystarczyło postracac i mamy funkcje kwadratowa

Basia: To moze MπM pokazesz to rozwiazanie ?

Eta: Łatwo krytykować , trudniej samemu rozwiązać!

Eta: Dobranoc Basiu

Basia: Bzdury kompletne. Nie przejmuj sie Eto. Zadnego rownania kwadratowego tam nie uzyskasz (a jezeli to bledne)

Basia: Dobranoc

Eta: Jasne,że tak

Basia: Robilam troche inaczej. Prosta przechodzi przez p−ty (x₀; f(x₀)) i (−3;1/2) stad

	1   −f(x0) 2
a =
	−3−x0

rownoczesnie a=f'(x₀) stad

1   −f(x0) 2
	= f'(x0)
−3−x0

1
	−f(x0) = (−3−x0)*f'(x0)
2

po podstawieniu i przeksztalceniu dostaje rownanie 3x₀³−x₀−2=0 (x₀−1)(3x₀²+3x₀+2)=0 x₀=1

	1
a=f'(1) = −
	3

	1
y = −		x+b
	3

1
	=1+b
2

	1
b=−
	2

	1		1
y = −		x−
	3		2