geometria pilne
miki: zad1
w Trójkącie prostokątnym ABC , <C=90 wybrano pnkP ,dla którego trójkąty APB ,PBC, PCA
mają równe pola.Wiedząc że PA2 + PB2 =45 oblicz PC
zad2
w Trójkącie prostokątnym ABC , <C=90 BC<AC poprowadzono prostą przez wierzchołek C trójkąta
przecinającą przeciwprostokątną w pnkD takim ze
AD : DB = 2:1.Wiedząc ze BC=√3 i kąt DCB=30o oblicz AB
17 lut 21:34
Eta:
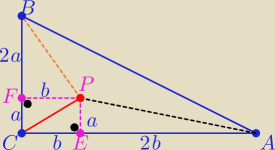
| | 1 | |
1/ z treści zadania P(APB)=P(PBC)=P(PCA)= |
| P(ABC) |
| | 3 | |
to |AC|=3b , |BC|=3a
Z tw. Pitagorasa w ΔAPE i BPF
|AP|
2=a
2+4b
2
|BP|
2=4a
2+b
2
+ −−−−−−−−−−−−−−−−−−−−−−−−
5a
2+5b
2=45 ⇒ a
2+b
2=9
to w ΔCPE : |CP|
2=a
2+b
2 =9 ⇒
|CP|=3
17 lut 22:48
iteRacj@:
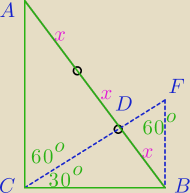
zad.2
|AD|=2*|DB|, AC∥FB
<FCA=60
o, <DFB=60
o,
<FDB i <ADC kąty wierzchołkowe
stąd ΔACD i ΔDFB (kkk) podobne w skali 2:1
|CB|=
√3
|FB|=|CB|*tg 30
o=1
|AC|=2*1=2
z tw. Pitagorasa dla ΔABC
|AB|
2=|CB|
2+|AC|
2=3+4=7
|AB|=
√7
17 lut 22:59
Eta:
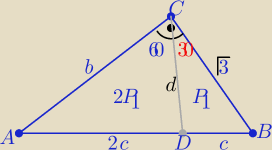
| | 1 | | 1 | |
2P1=2* |
| *b*d*sin60o i P1= |
| *d*√3*sin30o |
| | 2 | | 2 | |
to z tw. Pitagorasa |AB|=
√22+(√3)2=
√7
|AB|=√7
17 lut 22:59

 zad.2
|AD|=2*|DB|, AC∥FB
<FCA=60o, <DFB=60o,
<FDB i <ADC kąty wierzchołkowe
stąd ΔACD i ΔDFB (kkk) podobne w skali 2:1
|CB|=√3
|FB|=|CB|*tg 30o=1
|AC|=2*1=2
z tw. Pitagorasa dla ΔABC
|AB|2=|CB|2+|AC|2=3+4=7
|AB|=√7
zad.2
|AD|=2*|DB|, AC∥FB
<FCA=60o, <DFB=60o,
<FDB i <ADC kąty wierzchołkowe
stąd ΔACD i ΔDFB (kkk) podobne w skali 2:1
|CB|=√3
|FB|=|CB|*tg 30o=1
|AC|=2*1=2
z tw. Pitagorasa dla ΔABC
|AB|2=|CB|2+|AC|2=3+4=7
|AB|=√7
