trapez Tomek: W półokrąg o promieniu r wpisano trapez tak,że podstawa trapezu jest średnicą półokręgu wiedząc,że stosunek sumy długości podstaw trapezu do obwodu trapezu jest równy 2:3 Oblicz cosinus kąta ostrego trapezu

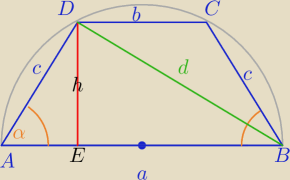
Mila: Podpowiedź:

a+b		2
	=		⇔a+b=4c z treści zadania
a+b+2c		3

	|AE|		a−b
1) W ΔAEB: cosα=		⇔cosα=
	c		2c

	c
2) W ΔDB: cosα=
	a

a−b		c
	=		i b=4c−a
2c		a

oblicz a w zależności od c i wstaw do (2)

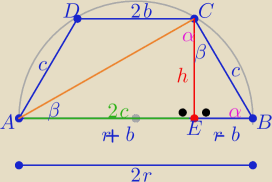
Eta: 1/ jak zwykle rysunek zgodny z treścią zadania i odpowiednie oznaczenia na nim

	2r+2b
z treści :		=2/3⇒ r+b=2c=|AE|
	2r+2b+2c

w ΔEBC : h=c*sinα

	sinα		2
w ΔAEC : tgα=2c/h ⇒		=		⇒ sin2α=2cosα
	cosα		sinα

to 1−cos²α=2cosα ⇒ cos²α+2cosα−1=0 , Δ=8, √Δ=2√2 cosα= −1−√2 −−− sprzeczność lub cosα= −1+√2 cosα= √2−1 ==========

Eta: Z jedynki trygonometrycznej: sin²α= 1−cos²α