Pochodne
Kalirr: Wyznacz przedziały monotonicznosci funkcji:
Tutaj pochodną liczyć ze wzoru na pochodną wymierna?
17 lut 17:13
Janek191:
Np. pochodna ilorazu

17 lut 17:21
Kalirr: | | −2x | |
Wychodzi f'(x) = |
| i z tego miejsce zerowe x=0 i funkcja jest rosnąca. Co robię |
| | (x2−4)2 | |
źle?
17 lut 17:40
Basia:
f'(x) policzyles dobrze
D = R\{−2;2)
znak pochodnej zalezy tylko od licznika bo mianownik jest stale dodatni
narysuj wykres y= −2x i zobacz
x∊(−∞;−2) ⇒ −2x>0 ⇒ f'(x)>0 ⇒ f rosnie
x∊(−2,0) ⇒ −2x>0 ⇒ f'(x)>0 ⇒ f rosnie
x∊(0;2) ⇒ −2x<0 ⇒ f'(x)<0 ⇒ f maleje
x∊(2;+∞) ⇒ −2x<0 ⇒ f'(x)<0 ⇒ f maleje
dla x=0 funkcja osiaga maksimum lokalne
17 lut 19:37
Kalirr: Dlaczego brane są pod uwagę przedziały od i do −2,2 skoro z f'(x)=−2x wynika że funkcja jest
dodatnia w przedziale (−∞;0) i ujemna (0;∞) ?
18 lut 15:51
Satan: To, że pochodna jest "dodatnia" nie znaczy, że funkcja jest. Pochodna to wyznaczanie jak szybko
zmieniają się wartości funkcji. One nie określają gdzie funkcja jest dodatnia, czy ujemna.
18 lut 15:59
Kalirr: Chodzi o to czy funkcja rośnie czy maleje. Nie jest tak, że gdy pochodna jest dodatnia w danym
przedziale to funkcja pierwotna w tym przedziale rośnie?
19 lut 11:16
Jerzy:
Nie widzisz,że funkcje nie istnieje w punktach: x = −2 oraz x = 2 ?
Funkcja jest rosnąca tam, gdzie pochodna jest dodatnie i odwrotnie.
19 lut 11:30
PW:
Częsta przyczyna złych wniosków to stosowanie twierdzenia zwanego warunkiem dostatecznym
monotoniczności bez uwzględnienia jego założeń.
Twierdzenie jest sformułowane dla przedziału otwartego. Jeżeli dziedzina funkcji składa się z
kilku rozłącznych przedziałów otwartych, to twierdzenie działa na każdym z nich z osobna − nie
działa na całej dziedzinie.
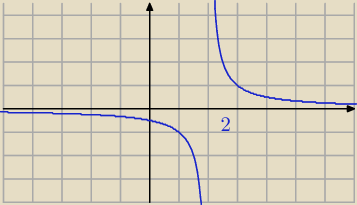
Funkcja na ilustracji ma pochodną ujemną na przedziale (−
∞, 2) i ma pochodną ujemną na
przedziale (2,
∞). Poprawny wniosek: funkcja jest malejąca na każdym z tych przedziałów. Nic
nie można wnioskować o zachowaniu funkcji w całej dziedzinie (ta jak widać nie jest malejąca w
całej dziedzinie R\{2}).
19 lut 11:47

 Częsta przyczyna złych wniosków to stosowanie twierdzenia zwanego warunkiem dostatecznym
monotoniczności bez uwzględnienia jego założeń.
Twierdzenie jest sformułowane dla przedziału otwartego. Jeżeli dziedzina funkcji składa się z
kilku rozłącznych przedziałów otwartych, to twierdzenie działa na każdym z nich z osobna − nie
działa na całej dziedzinie.
Funkcja na ilustracji ma pochodną ujemną na przedziale (−∞, 2) i ma pochodną ujemną na
przedziale (2,∞). Poprawny wniosek: funkcja jest malejąca na każdym z tych przedziałów. Nic
nie można wnioskować o zachowaniu funkcji w całej dziedzinie (ta jak widać nie jest malejąca w
całej dziedzinie R\{2}).
Częsta przyczyna złych wniosków to stosowanie twierdzenia zwanego warunkiem dostatecznym
monotoniczności bez uwzględnienia jego założeń.
Twierdzenie jest sformułowane dla przedziału otwartego. Jeżeli dziedzina funkcji składa się z
kilku rozłącznych przedziałów otwartych, to twierdzenie działa na każdym z nich z osobna − nie
działa na całej dziedzinie.
Funkcja na ilustracji ma pochodną ujemną na przedziale (−∞, 2) i ma pochodną ujemną na
przedziale (2,∞). Poprawny wniosek: funkcja jest malejąca na każdym z tych przedziałów. Nic
nie można wnioskować o zachowaniu funkcji w całej dziedzinie (ta jak widać nie jest malejąca w
całej dziedzinie R\{2}).