Stereometria - ostrosłup
UczącySię: W ostrosłupie prawidłowym czworokątnym odległości środka wysokości od krawędzi bocznej i ściany
bocznej wynoszą odpowiednio a oraz b. Wyznacz objętość ostrosłupa i podaj warunek
rozwiązalności zadania.
oznaczyłem sobie krawędź podstawy jako c i dostałem, że
c = 4b = 2√2a. Z tego chyba mógłbym policzyć sobie podstawę, ale nie wiem jak policzyć
wysokość i czy moje wcześniejsze obliczenia są poprawne
17 lut 14:15
Basia:
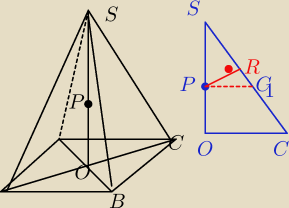
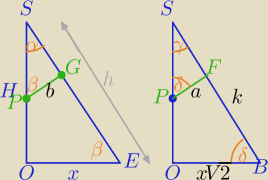
A,B,C,D srodki krawedzi bocznych
| | c√2 | | c√2 | |
a = |SC| = U{1}[2}* |
| = |
| |
| | 2 | | 4 | |
4a = c
√2
c = 4b
tak liczyles, a mnie sie wydaje, ze to nie tak
wg mnie a to dlugosc odcinka PR
zeby znalezc b trzeba przez P poprowadzic prosta prostopadla do plaszczyzna BSC
i na razie nie wiem jak to powinno wygladac
17 lut 20:58
Mila:
Masz odpowiedź. Mam obliczenia, ale dość rozbudowany wzór na końcu.

17 lut 21:18
Mila:
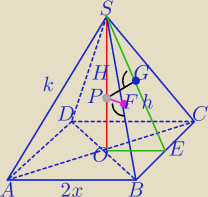
|PF|=a, |PG|=b, AB=2x, |OS|=H
|OB|=x
√2, |OE|=x
1)
Pole ΔSOB na dwa sposoby i tw. Pitagorasa:
|OB|*H=|SB|*a
x
√2*H=k*a i H
2+(x
√2)
2=k
2⇔
| | x√2*H | | 2x2*H2 | |
k= |
| i H2+2x2= |
| |
| | a | | a2 | |
| | 2x2 | | 2x2−a2 | |
2x2=H2*( |
| −1)⇔2x2=H2* |
| |
| | a2 | | a2 | |
===================
2) Pole ΔSOE na dwa sposoby i tw. Pitagorasa:
|OE|*H=h*b i H
2+x
2=h
2
| | x*H | | x2*H2 | |
x*H=h*b⇔h= |
| i H2+x2= |
| stąd |
| | b | | b2 | |
================
3) porównanie H
| 2x2*a2 | | x2*b2 | |
| = |
| stąd |
| 2x2−a2 | | x2−b2 | |
| | a2 | |
H2=2x2* |
| po podstawieniu za x2 |
| | 2x2−a2 | |
4)
| | 1 | | 1 | | 4a2b2 | | a*b | |
V= |
| *(2x)2*H= |
| * |
| * |
| |
| | 3 | | 3 | | 2a2−2b2 | | √2b2−a2 | |
| | 2a3*b3 | |
V= |
| |
| | 3*(a2−b2)*√2b2−a2 | |
=========================
17 lut 21:53
Mila:
PF⊥SB, PG⊥SE
17 lut 22:07
UczącySię: Odpowiedź mam i wynosi :
| | 16a3b3 | |
|
| |
| | 3(a2 − b2)√2b2 − a2 | |
17 lut 22:17
Mila:
To szkoda, że wcześniej nie podałeś. Szukaj, gdzie coś pominęłam w rachunkach.
Ja dopiero jutro mogę .
17 lut 22:42
Mila:
Nie znalazłeś błędu?
18 lut 15:32
Mila:
Poprawka
1) Pole ΔSOB na dwa sposoby i tw. Pitagorasa:
|OB|*H=|SB|*
2a ( zastanów się dlaczego ? )
x√2*H=k*2a i H
2+(x√2)
2=k
2
stąd:
2)
Pole ΔSOE na dwa sposoby i tw. Pitagorasa:
|OE|*H=h*
2b i H2+x2
=h
2
3) porównanie H
2
| 4x2*a2 | | 4x2*b2 | |
| = |
| |
| x2−2a2 | | x2−4b2 | |
==============
==========
4)
| | 1 | | 2a2b2 | | 2a*b | |
V= |
| *4* |
| * |
| |
| | 3 | | a2−b2 | | √2b2−a2 | |
| | 16a3*b3 | |
V= |
| |
| | 3(a2−b2)*√2b2−a2 | |
=======================
18 lut 15:51
UczącySię: No racja, to jest błąd, ale trochę nie jestem przekonany, bo przecież pole SOB
| (|OB| * H) | |
| ... ale czy to równa się SB * a ? Bo odcinek a nie jest przecież wysokością |
| 2 | |
18 lut 17:14
UczącySię: Dobra, już widzę, a jest przecież jakby połową wysokości
18 lut 17:15
Mila:
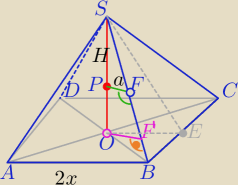
PF nie jest wysokością
P jest środkiem OS.
PF⊥SB
|PF|=a
OF' || PF ⇒OF'=2a i OF' jest wysokością w ΔSOB poprowadzona z wierzchołka O do boku SB
|OB|=x
√2
x
√2*H=k*2a
w podobny sposób postąpimy z ΔSOE
II sposób
Skorzystaj z podobieństwa ΔSPF i SOB i tw. Pitagorasa.
Skorzystaj z podobieństwa ΔSPG i SOE i tw. Pitagorasa. rysunek porzedni.
Widzę, że jesteś ambitnym uczniem, więc do pracy.
Jeśli nie wyjdzie , to pomogę.
Najpierw przelicz I sposób, jeśli jeszcze będą pytania to pisz,
jestem na forum ( aczkolwiek z przerwami)
18 lut 17:33
UczącySię:
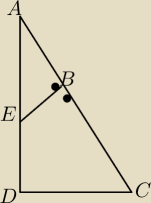
EB = b
c − krawędź podstawy
Czy w tym drugim sposobie chodzi o takie coś ?
18 lut 17:52
Mila:
|SE|=h
Dla uniknięcia ułamków, które utrudniają przekształcenia,
oznacz krawędź podstawy : 2x, albo 2c .
Trzymajmy się oznaczeń jak na rysunku 21:53.
1) W ΔSOE:
h
2=H
2+x
2
| b | | x | | 2b | | x | |
| = |
| ⇔ |
| = |
| |
| 0.5H | | h | | H | | √H2+x2 | |
2)W ΔSOB:
k
2=H
2+2x
2
| a | | x√2 | | 2a | | x√2 | |
| = |
| ⇔ |
| = |
| |
| | k | | H | | √H2+2x2 | |
teraz licz dalej, wiesz co ma wyjść.
18 lut 18:29
UczącySię: Okej, ale sam pomysł miałem dobry tak ?
18 lut 18:42
Mila:
Dobry.

18 lut 19:02
UczącySię: To super ! Dzięki za pomoc Milu

18 lut 19:57
 A,B,C,D srodki krawedzi bocznych
A,B,C,D srodki krawedzi bocznych

 |PF|=a, |PG|=b, AB=2x, |OS|=H
|OB|=x√2, |OE|=x
1)
Pole ΔSOB na dwa sposoby i tw. Pitagorasa:
|OB|*H=|SB|*a
x√2*H=k*a i H2+(x√2)2=k2⇔
|PF|=a, |PG|=b, AB=2x, |OS|=H
|OB|=x√2, |OE|=x
1)
Pole ΔSOB na dwa sposoby i tw. Pitagorasa:
|OB|*H=|SB|*a
x√2*H=k*a i H2+(x√2)2=k2⇔
 PF nie jest wysokością
P jest środkiem OS.
PF⊥SB
|PF|=a
OF' || PF ⇒OF'=2a i OF' jest wysokością w ΔSOB poprowadzona z wierzchołka O do boku SB
|OB|=x√2
PF nie jest wysokością
P jest środkiem OS.
PF⊥SB
|PF|=a
OF' || PF ⇒OF'=2a i OF' jest wysokością w ΔSOB poprowadzona z wierzchołka O do boku SB
|OB|=x√2

 |SE|=h
Dla uniknięcia ułamków, które utrudniają przekształcenia,
oznacz krawędź podstawy : 2x, albo 2c .
Trzymajmy się oznaczeń jak na rysunku 21:53.
1) W ΔSOE:
h2=H2+x2
|SE|=h
Dla uniknięcia ułamków, które utrudniają przekształcenia,
oznacz krawędź podstawy : 2x, albo 2c .
Trzymajmy się oznaczeń jak na rysunku 21:53.
1) W ΔSOE:
h2=H2+x2

