Metody Numeryczne - przybliżenie pochodnych, wzór róznicowy i siatka Stachu: Zadanie z Metod Numerycznych. Nie wiem czy dobrze rozwiązuję zadania tego typu, czy ktoś mógłby pomóc? Zadanie dzieli się na dwie części: 1. Dana jest funkcja u(x,y)=u(x_i,y_j)≈u_{i, j}. Zapisać kolejno dla u(x,y)=u(x_i,y_j)≈u_{i, j} wzory na przybliżenie pochodnych: A. pierwszego rzędu, względem zmiennej y na podstawie wzoru:

	F(t) − F(t−Δt)
F'(t)≈
	Δt

B. drugiego rzędu, względem zmiennej x na podstawie wzoru:

	F(t) − 2F(t+Δt)+F(t+2Δt)
F''(t)≈
	Δt2

Tę część rozwiązałem następująco:

	F(t) − F(t−Δt)
A. F'(t)≈
	Δt

du		u(x,y) − u(x,y−Δy)		u(xi,yj) − u(xi,yj−1)
	≈		=		=
dy		Δy		Δy

	ui,j−ui,j−1
	Δy

	F(t) − 2F(t+Δt)+F(t+2Δt)
B. F''(t)≈
	Δt2

d2u		u(x,y) − 2u(x+Δx,y) +u(x+2Δx,y)
	≈		=
dx2		Δx2

	u(xi,yj)−2u(xi+1,yj)+u(xi+2,yj)		ui,j−2ui+1,j+ui+2,j
		=
	Δx2		Δx2

2. Dana jest funkcja u(x,y)=u(x_i,y_j)≈u_{i, j} spełniająca zagadnienia brzegowe:

d2u		du
	− RC		+ u = 0
dx2		dy

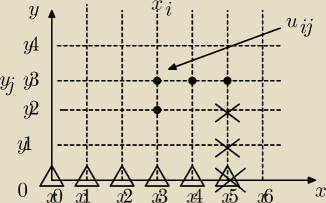
u(x,0)=Δ, dla x∊[0,5] u(5,y)=X, dla y∊[0,2] A. Utworzyć wzór różnicowy dla podanego równania różniczkowego, korzystając ze wzorów z części 1 zadania. B. Narysować siatkę. Zaznaczyć na niej wszystkie wprowadzone oznaczenia, punkty tworzące otrzymany wzór różnicowy oraz warunki brzegowe. Przyjąć podział siatki na 6 części względem zmiennych x i y. Tę część rozwiązałem następująco: A. Na podstawie powyższych wzorów na przybliżenie pochodnych:

	d2u		du
		− RC		+ u = 0 ⇒
	dx2		dy

	ui,j−2ui+1,j+ui+2,j		ui,j−ui,j−1
⇒		− RC		+ ui,j = 0
	Δx2		Δy

B. Starałem się przedstawić najlepiej jak umiem na rysunku. Same zaznaczenie punktów wydaję mi się że rozumiem. Nie jestem jednak pewien zagadnień brzegowych.