Dany jest graniastosłup prawidłowy trójkątny Maturzysta2018: Dany jest graniastosłup prawidłowy trójkątny, którego suma długości wszystkich krawędzi wynosi L. Oblicz, jakie muszą być długości krawędzi, aby pole powierzchni bocznej było największe. Mam na razie: L=6a+3h 3h=L−6a Ppb= 3ah= 3a(L−6a)= 3aL−18a² Co dalej, bo szczerze mówiąc zgłupiałem?

lanza: https://www.zadania.info/d626/9963310 tu jest podobne

Maturzysta2018: Dobra, źle już zacząłem robić w momencie podstawiania

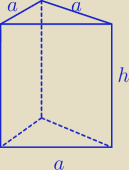
Mila: L=6a+3h L−6a=3h

	1
L−6a>0⇔a<		L
	6

P_b=3a*h=a*(3h) P_b(a)=a*(L−6a)=L*a−6a² parabola skierowana w dół P_b(a) przyjmuje największą wartość w wierzchołku paraboli

	−L		L
aw=		=
	−12		12

	1		1		L		1
wtedy h=		L−2aw=		L−2*		=		L
	3		3		12		6

odp.

	L
a=
	12

	1
h=		L
	6

Posprawdzaj rachunki.

Maturzysta2018: Dziękuję bardzo Mila! Wszystko rzetelnie i dokładnie. Jak zwykle w formie. Jeszcze raz dzięki

Mila: