Wyznacz ilość rozwiązań w zależności od parametru a Maciess: Stare zadanko z konkursu. Myślałem ze najlepiej będzie to robić graficznie.

⎧	|x|+|y|=1
⎩	|x|+a=y

Drugie równanie to rozumiem mam wykres y=|x| i parametr a "przesuwa go w góre lub w dół" A jak samemu wyrysować ten pierwszy wykres? Programik mi wyrysował tą funkcje i wyszedł kwadracik o wierzchołkach (−1,0) ,(0,1),(1,0),(0,−1) Czyli wg mnie odpowiedź to a=1 mamy jedno rozwiązanie a∊(−1,1) układ ma dwa drozwiązania a=−1 jest nieskończenie wiele rozwiązań, bo proste się pokrywają i zbiór jest niepoliczalny (nie wiem jak to ładnie zapisac) I prośba do was jakby ktoś mi wytłumaczył jak narysować ten pierwszy wzór, bo cięzko mi sobie to wyobrazić

Blee: Pierwszy zbior ... rozpatrujesz cztery przypadki: 1) x>0 y>0 x+y = 1 −> y = −x +1 Rysujesz prosta Analogicznie pozostale przypadki Tak naprawde tez mozesz zauwazyc ze przypadek x>0 y<0 to odbicie pierwszego przypadku wzgledem osi OY Dwa pozostale to odbicia tych dwoch wzgledem osi OX. Albo tak jak pisalem − rozpatrujesz pokolei te przypadki i masz kwadracik

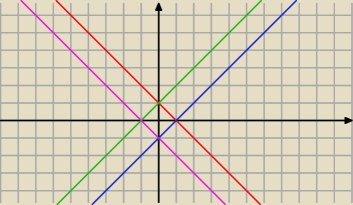
yy: ROZPISZE TYLKO |x| + |y| = 1 −−> Rysunek tez tylko do tego mozesz to zrobic chocby tak: |x| + |y| = 1 x moze byc dodatnie i ujemne, tak samo igrek (wlasciwie nieujemne i ujemne xd) zatem mamy takie 4 przypadki 1) x ≥ 0 i y ≥ 0 2) x ≥ 0 i y < 0 3) x < 0 i y ≥ 0 4) x < 0 i y < 0 zatem rozpiszmy troszke 1) x ≥ 0 i y ≥ 0, wtedy |x| = x, |y| = y x+y=1 −−> y = −x + 1 <−− trzeba narysowac prosta 2) x ≥ 0 i y < 0, wtedy |x| = x, |y| = − y x−y=1 −−> y = x−1 <−−rysujemy 3) x < 0 i y ≥ 0, wtedy |x| = − x, |y| = y −x+y=1 −−> y = x+1 <−−rysujemy 4) x < 0 i y < 0, wtedy |x| = −x, |y| = −y −x−y=1 −−> y = −x−1 <−−rysujemy Po narysowaniu tych czterech prostych wybieramy to co w srodku bedzie, czyli ten obrocony kwadrat. a jak sprawdzic czy sie zgadza na pewno, mozna podstawic np. za x = 0, wtedy |y| = 1, y = − 1 lub y=1 (patrzymy czy dla x=0 mamy dwa igreki − y=1 oraz y=−1 zatem odp. brzmi tak)

Maciess: Czyli na przedziałach. zastanawiałem się jak uzasadnić że to akurat ten kwadracik będzie wykresem. Dziękuje bardzo Blee i yy. Dobranoc

Adam0: tak, ale prościej rozpatrywać tylko 2 przypadki y≥0 i y<0 przecież wiadomo jak y=|x| wygląda

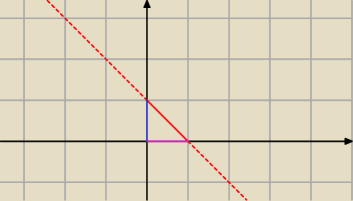
yy: oczywiscie zamiast rysowania calych prostych mozna odpowiednie fragmenty wtedy rysunek czytelniejszy troche. np. 1) x ≥ 0 i y ≥ 0 oraz prosta wyszla : y = − x + 1 wiec wystarczy zaczac od punktu (0,0) i skoro zarowno x >=0 jak i y >=0 to wiadomo ze to bedzie cwiartka numer jeden jedynie wiec mozna zaznaczyc ten trojkat az do prostej y=−x+1 wystarczy ten ciagly czerwony fragment zaznaczyc (zamiast tej calej prostej) i mamy taki trojkat.

yy: oczywiscie jak sie juz ma wprawe to mozna tak jak @Adam zaproponowal. czyli np. 1) x ≥ 0 2) x < 0 i wtedy dla 1) gdzie x ≥ 0 mamy |x| = x, zatem x + |y| = 1 −−> |y| = 1−x i teraz z definicji wartosci bezwzglednej |y| = a −−> y = −a lub y = a zatem y = 1−x lub y = −1+x i 2)... i tyle