Dowód alfa beta gamma
Carry: Dobry wieczór,
mam problem z zadaniem:
jeżeli x,y,z są miarami kątów wewnętrznych trójkąta i sin
2x+sin
2y<sin
2z
Pokaż, że cosz<0
Próbowałem to rozpisać na wiele sposobów i nic mi nie wychodzi
Liczę na odpowiedź i pomoc w zrozumieniu
13 lut 22:49
Helena Paździochowa: spróbuj z tw.sinusów dla kąta x np.bok naprzeciwko niego niech będzie a naprzeciwko kąta y bok
b a naprzeciwko kąta z bok c.I później z twierdzenia cosinusów wyznacz cos z
13 lut 22:51
Blee:
sinz = sin(180 − (x+y)) = sin(x+y) = sinx*cosy + cosxsiny
sin2z = sin2xcos2y + 2sinxcosxsinycosy + sin2ycos2x
więc mamy:
sin2x + sin2y < sin2xcos2y + 2sinxcosxsinycosy + sin2ycos2x
sin2x(1−cos2y) + sin2y(1−cos2x) < 2sinxcosxsinycosy
sin2xsin2y + sin2y*sin2x < 2sinxcosxsinycosy
2sin2xsin2y < 2sinxcosxsinycosy
sinxsiny < cosxcosy
sinxsiny − cosxcosy < 0
−(cos(x+y)) < 0
cos(180 − (x+y)) < 0
cosz < 0
c.n.w.
13 lut 22:55
Blee:
wykorzystane wzory:
dwa wzory redukcyjne
wzór na sinusa sumy kątów
wzór na cosinusa sumy kątów
13 lut 22:56
Mila:
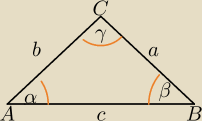
1) Rodzaje trójkątów i tw. odwrotne do tw. Pitagorasa.
2) Twierdzenie sinusów
| a | | b | | c | |
| = |
| = |
| =2R |
| sinα | | sinβ | | sinγ | |
R− promień okręgu opisanego na Δ
| | a | | b | | c | |
sinα= |
| i sinβ= |
| i sinγ= |
| |
| | 2R | | 2R | | 2R | |
Z zał.
a
2+b
2<c
2⇔Δ jest rozwartokątny ⇔cosγ<0
13 lut 23:16
Carry: Wielkie dzięki Blee <3
13 lut 23:17
Carry: i MIla za drugi sposób rozwiązania :3
13 lut 23:17
Helena Paździochowa: A ja ?
13 lut 23:18
Carry: Haha, również
, nie zauważyłem Twojego wpisu wcześniej, przepraszam
13 lut 23:19
Helena Paździochowa:
13 lut 23:19