f kwadratowa z parametrem ans: wyznacz wszystkie wartości parametru m dla których funkcja mx²+x+m−1 ma dwa rózne miejsca zerowe, z których każde jest mniejsze od 1 1)Δ>0

	1−√2		1+√2
m∊(		,		)
	2		2

2)m≠0 3)X1<1, X2<1 no i wyznaczylem p<1

X1+x2
	<1
2

−b
	<2
a

−1
	<2
2m

jak zrobić założenia, bo mnożąc nierówność przez 2m nie wiemy czy jest dodatnie czy ujemne.

Blee: 1) ok 2) ok 3) z viete'a tego nie zrobisz Musisz poradzic sobie za pomoca funkcji f(x) Dla m>0 wierzcholek dla x<1 i f(1)>0 Dla m<0 wierzcholek dla x<1 i f(1) <0

ans: hmm dalej mi nie wychodzi, mógłbyś to rozwiązać?

ans:

	−1
ciągle mi wychodzi		<1
	2m

	−4m2+4m+1
albo		<0
	4m

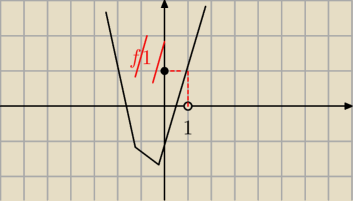
Timor i pumba: dla m>0 Δ>0 f(1)>0 x_w<1 Delta rozwizana f(1)= m*1²+1−m−1>0 to rozwiaz sobie x_w<1

−1
	<1
2m

Przeciez m>0 to zwrot nierownosci sie nie zmieni jesli obie strony pomnozysz przez 2m Dla m<0 Δ>0 ( ale to juz masz zrobione f(1)<0 czyli m*1²+1−m−1<0 x_w<1

−1
	<1
2m

Tu juz sie zwrot zmieni bo m<0 Rozwiazujesz te wszystkie warunki ladujesz na os liczbowa i odczytujesz rozwiazanie Masz rysunek do a) gdzie m>0 Juz widzac dlaczego te warunki czyli f(1)>0 i w_x<1 Ty sobie zrob rysunek dla m<0

ans:

	1−√2		1+√2
ok wszystko rozumiem wyszlo mi m∊(		,		) zas w odp jest m∊(0,
	2		2

	1+√2
		) tak jaby nie brali pod uwagę m<0.
	2

Blee: x_wierzchołka < 1

−b
	< 1
2a

−1
	< 1
2m

dla m>0 −> 2m > −1 (zawsze spełnione) dla m<0 −> 2m < −1 −> m < −1/2 ... a dla takiego m przecież Δ <0

	1−√2		1 − √4		1 − 2		1
zauważ, że		>		=		= −
	2		2		2		2

Blee: dlatego wariant z m<0 nie daje żadnego rozwiązania

ans: teraz jasne, dzięki