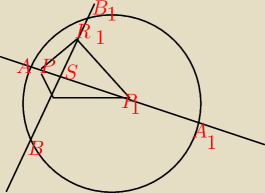
 Przez punkt S poprowadzono dwie proste, które przecięły okrąg o w punktach A, A1
oraz B, B1 jak na rysunku obok. Punkty P, P1, R, R1 oznaczają odpowiednio
środki odcinków SA,SA1, SB' SB1. Wykaż, że na czworoącie PRP1R1 można opisać okrąg
Przez punkt S poprowadzono dwie proste, które przecięły okrąg o w punktach A, A1
oraz B, B1 jak na rysunku obok. Punkty P, P1, R, R1 oznaczają odpowiednio
środki odcinków SA,SA1, SB' SB1. Wykaż, że na czworoącie PRP1R1 można opisać okrąg
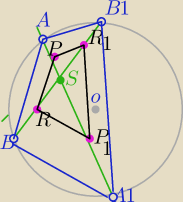 1) W ΔABS zostały połączone środki boków zatem odcinek PR jest równoległy do AB i równy
połowie AB.
Analogicznie postąpiono w ΔA1B1S, ΔAB1S,ΔA1BS.
1) W ΔABS zostały połączone środki boków zatem odcinek PR jest równoległy do AB i równy
połowie AB.
Analogicznie postąpiono w ΔA1B1S, ΔAB1S,ΔA1BS.
| 1 | ||
Czworokąt PRP1R1 jest podobny ( jest jednokładny) do ABA1B1 w skali k= | ||
| 2 |