pole figury mat: Dana jest figura f określona nierównością x²+y²+4x−6y−3≤0 Oblicz pole figury która jest sumą figury f i figury powstałej z f przez symetrię osiową o osi OY Dla mnie to istny kosmos pomoże ktoś bardzo proszę

Timor i pumba: x²+y²+4x−6y−3≤0 to jest kolo o srodku S=(−2,3) i promieniu r=4

mat: Rysunek to ja też mam taki sam ale jak dalej................

Blee: 1) wyznaczasz punkty przecięcia się okręgu f z osią OY 2) Obliczasz pole wycinka okręgu który wychodzi na ujemną stronę osi OX 3) Odejmujesz tą wartość od pola całego okręgu 4) Otrzymaną wartość mnożysz przez 2 i masz rozwiązanie

Mila:

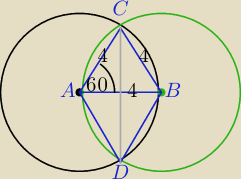
	120		16
P(wyc.CAD)=		π*42=		π
	360		3

	16π
Podcinka kołaCDB=		−PΔCAD=
	3

	16π		1		16π
=		−		*42*sin120o=		−4√3
	3		2		3

Pole soczewki ADBC:

	16π		32π
Psocz.=2*(		−4√3)=		−8√3
	3		3

P_figury=2π*4²−P_socz.

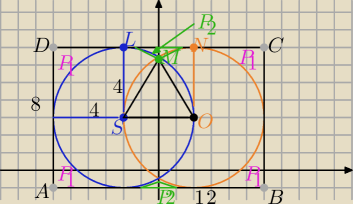
Eta: P= P▭(ABCD) − 4P₁−2P₃ r=4 S(−2,3) Wymiary prostokąta : 8 i 12 to P▭=96 P₁= P□ − (1/4)πr² to 4P₁= = 64−16π następnie P₃ obliczamy tak:

	r2√3
ΔSCM jest równoboczny o boku r=4 PΔ=		= 4√3
	4

i mamy dwa przystające wycinki SLM i ONM o kącie środkowym 30^o

	1		1		8π
o polach		πr2 to obydwa mają pole		πr2 =
	12		6		3

	8π
P3= P□(SONL) − PΔ−
	3

zatem

	8π
P( figury) =96 −(64−16π) −		=.....................
	3

Eta: Ajjj w P₃ zapomniałam o P_Δ Myślę,że już sam dokończysz