równanie wielomianowe z wartością bezwzględną
QWERTY: |x3−x|+x2−1=0
12 lut 20:00
Adam0: |x|*|x2−1|+x2−1=0
x2−1=0 lub (x2−1>0 oraz |x|+1=0) lub (x2−1<0 oraz |x|−1=0)
x=±1 (bo |x|+1 − sprzeczne, a z |x|=1 i tak wychodzi x=±1)
12 lut 20:13
Adam0: |x|+1=0 − sprzeczne
12 lut 20:14
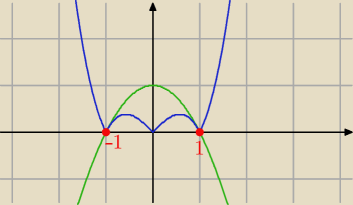
Eta:
12 lut 20:15
Vobro: Na przedziały?
x3−x=0
x(x2−1)=0
x(x−1)(x+1)=0
x=0 v x=1 v x=−1
Przedziały będą takie
1ox∊(−∞,−1)
2ox∊<−1,0)
3ox∊<0,1)
4ox∊<1,+∞)
12 lut 20:15
PW: Jeszcze raz pokażę, że zanim rzucimy się na rachunki, warto o chwilę namysłu (a QWERTY i tak
nie posłucha).
|x(x2−1)|=−x2+1.
Lewa strona jest liczbą nieujemną dla dowolnej x. Rozwiązania mogą więc istnieć tylko, gdy
prawa strona jest nieujemna:
(1) −x2+1≥0.
|x| |x2−1|=−x2+1
− dla x spełniających nierówność (1) jest
|x|(−x2+1)=−x2+1
Rozwiązaniami są takie x, dla których
−x2+1=0,
to znaczy (−1) lub 1. Dla pozostałych x po podzieleniu stronami otrzymamy równanie
|x|=1,
które nie ma nowych rozwiązań.
12 lut 20:40
QWERTY:
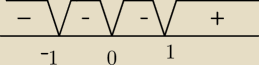
x=−1 ∧ x=1
12 lut 20:40

 x=−1 ∧ x=1
x=−1 ∧ x=1