Układ równań UczącySię: Rozwiąż układ równań i zbadaj liczbę rozwiązań równania w zależności od parametru m: 1. x² + y² −4= 0 2. x +y −m = 0 To są te dwa równania spięte klamrą I teraz czy ja mam z nich wyliczyć y ?

blx: Z równania 2. wyznacz y i wstaw do pierwszego, otrzymasz tym sposobem sparametryzowane równanie kwadratowe. Wtedy wystarczy rozważyć znak delty.

PW: Dobrze by było narysować w układzie współrzędnych, co to znaczy. Pierwsze równanie opisuje okrąg o środku (0, 0) i promieniu 2. Drugie równanie to prosta zależna od parametru m. Od razu widać, czego się można spodziewać.

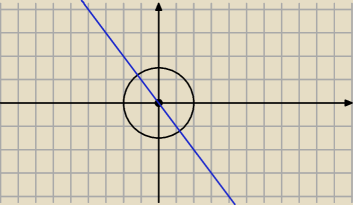
Krzysiek60: Odpoczene chwile od kombinatoryki Zauwaz z ete dwa rownania przedstawiaja 1 okrag o srodku (0,0) i pronieniu r=2 2 to prosta y=−x+m Musisz sobiezrobic dokladny rysunek cos mi tutaj nie wychodzii niebieska to y=−x teraz tak musisz dobrac m zeby byly dwa punkty przeciecia okregu z prosta , 1 punk i dla pewnego m nie ma punktow wspolych .

UczącySię: PW ale czy druga prosta nie jest zależna od x i m ?

PW: Prosta ma równanie y=−x+m. W zależności od wartości parametru m będzie się przesuwała w górę lub w dół. Krzysiek narysował ją dla m=0.

UczącySię: Krzysiek dzięki Jednakże dobranie tego m raczej z rysunku nie wyjdzie

UczącySię: Już wyszło, dzięki wszystkim za pomoc! Zadanie w sumie proste

piotr: można i z rysunku odczytać m (bo jest łatwy kąt nachylenia prostej) dwa rozwiązania: m∊(−2√2; 2√2) jedno m= −2√2 ∨ m = 2√2 dla pozostałych m brak rozwiązań