Geo Michał: Punkty A, B, C są wierzchołkami trójkąta równoramiennego ABC, w którym punkt D jest środkiem podstawy AB. Punkt K− z kolei− jest symetryczny do punktu D względem prostej AC, punkt L−symetryczny do punktu D względem prostej BC. Oblicz odległość punktów K i L, jeśli |AB| = |CD| = 10dm

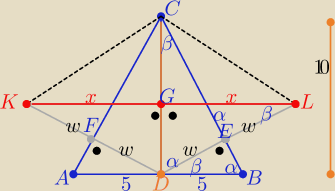
Eta: 1/ Szukana długość |KL|=2x |AB|=10=|DC| to |BC|=√100+25= 5√5 |DL=2w

	1		1
P(BDC)=		*5*10= 25 i P(BDC)=		w*|BC|
	2		2

to w*5√5= 50 ⇒ w= 2√5 to 2w=4√5 Zauważ trójkąty podobne ΔDLG i BDC z cechy (kkk)

	4√5		4
to		=		=k −−− skala podobieństwa
	5√5		5

zatem x= |DC|*k ⇒ x= 8 to |KL|=2x= 16 dm ================