Geo Michał: Czworokąt ABCD, w którym |AB|= 1dm, |BC| = 2dm, |CD| = 3dm, jest wpisany w okrąg i jego przekątne są prostopadłe. Oblicz pole tego czworokąta

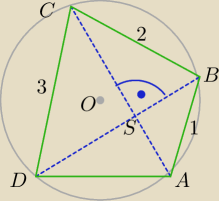
iteRacj@: ΔABS, ΔBCS, ΔCDS, ΔADS prostokątne z tw.Pitagorasa dla tych trójkątów |SA|²+|SB|²=1² |SC|²+|SB|²=2² |SC|²+|SD|²=3² |SA|²+|SD|²=|AD|² stąd |SA|²+|SB|²+|SC|²+|SD|²=3²+1² (|SA|²+|SD|²)+(|SB|²+|SC|²)=10 |AD|²+4=10, |AD|>0 |AD|=√6 z tw. Ptolemeusza |AC|*|BD|=|AB|*|CD|+|CB|*|AD| = 1*3+2*√6

	1		1		1
PABCD=		*|AC|*|BD|*sin 90o=		*|AC|*|BD|=		*(1*3+2*√6)
	2		2		2