Sześciokąt wypukły Michał: Dany jest sześciokąt wypukły ABCDEF o kątach przy wierzchołkach A, B, C, D równych odpowiednio 90◦, 128◦, 142◦, 90◦. Wykaż, że pole tego sześciokąta jest mniejsze

	1
niż		*AD2. Przerabiam zadania z OMG i mam problem z tym właśnie.
	2

Eta:

	1
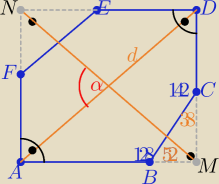
Pole prostokąta AMDN : P=		d*d*sinα , d= |AD|
	2

ponieważ sześciokąt zawiera się w tym prostokącie

	1
to jego pole jest <		d2*sinα i sinα<1
	2

	1
zatem P(ABCDEF) <		|AD|2
	2

Eta: Jeszcze trzeba uzasadnić dlaczego czworokąt AMDN jest prostokątem a to już proste ... napisz odpowiedni komentarz

Michał: Ponieważ ma dwa boki parami równoległe i dwa kąty proste?

Michał: Trzy kąty proste*, z czego wynika że czwarty też jest prosty