Podaj wartość tangensa kąta "alfa" + braki w wiedzy na temat trygonometrii Fuchs: Zadanie: Jedno ramię kąta "alfa" zawiera się w dodatniej półosi OX, a drugie leży w II ćwiartce układu współrzędnych i zawiera się w prostej o równaniu y= − ²₃x. Podaj wartość tangensa kąta "alfa". Pytanie: Witam wszystkich, mam problem (a nawet trzy). Po pierwsze, nie jestem pewien czy dobrze rozumiem pojęcia sinusa i cosinusa. Czy sinus to współrzędna "igrekowa" punktu, który znajduje się na przecięciu ramienia kąta (tego, który nie zawiera się w osi układu współrzędnych) z okręgiem jednostkowym, a cosinus to współrzędna "iksowa" tego punktu? Czy jeśli liczę sinus i cosinus kąta, to w praktyce szukam współrzędnych właśnie tego punktu i to właśnie jest sedno tych obliczeń? Po drugie: Obliczyłem tangens kąta, o który pytają w zadaniu. Wyszło mi −²₃. Najpierw policzyłem wartość funkcji f(x)= − ²₃x dla argumentu −1, ponieważ okrąg jednostkowy będzie przechodził przez punkt P(−1,0), a następnie podzieliłem wynik ( ²₃ ) przez −1 i otrzymałem tangens kąta alfa. Wynik zgadza się z odpowiedziami z tyłu książki, ale jest tam również dopisek: Współczynnik kierunkowy prostej równy jest tangensowi kąta nachylenia prostej do osi OX, więc tg"alfa"= − ²₃. Nie wiem czy to jest jakaś ogólna reguła, ale jeśli tak, nie wiem z czego ona wynika. Czy ktoś mógłby mi to wytłumaczyć? Trzeci problem polega na tym, że w właściwie nie wiem czy dobrze myślałem podczas rozwiązywania tego zadania i czy poprawny wynik nie wyszedł mi przypadkiem. Bardzo proszę o pomoc.

Basia: wszystko co piszesz jest zgodne z prawdą, ale strasznie sobie życie komplikujesz jeżeli masz prostą y=ax+b to tgα=a gdzie α − kąt nachylenia prostej do osi OX jeżeli chodzi o definicje funkcji trygonometrycznych radziłabym oswoić się z definicją nieco bardziej ogólną

	y		x		y		x
sin α=		; cos α=		, tg α=		; ctg α=
	r		r		x		y

gdzie P(x,y) dowolny ≠O punkt na końcowym ramieniu kąta r=|OP|

Fuchs: Aha, chyba rozumiem. Czyli gdybym zamiast f(x)=−²₃x miał f(x)=−²₃x + 1, to nie powinienem, analogicznie do tego co robiłem wcześniej, liczyć f(−1)=⁵₃, a potem dzielić tego przez −1, i twierdzić, że policzyłem tangens, bo teraz wykres znajduje się o 1 wyżej i jego drugie ramie nie leży już na osi OX, tylko na y=1? Czyli dalej tangens będzie równy −²₃ tylko cały wykres będzie wisiał wyżej? Tylko w takim razie, co liczyłem dzieląc ⁵₃ przez −1? I jak (jeśli dobrze rozumiem co się dzieje na wykresie) mam to wszystko zapisać za pomocą obliczeń?

Basia:

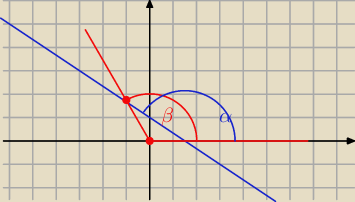
	2
niebieska prosta to Twoja prosta y=−		+1
	3

jej kąt nachylenia do OX to α

	5
dzieląc		przez −1 policzyłeś tgβ (ten zaznaczony na czerwono)
	3

Basia: zauważ, że proste

	2		2
y=−		x i y=−		x+1
	3		3

są równoległe ich kąty nachylenia do OX muszą być równe

Fuchs: Aha, i ramię kąta β zawierałoby się w prostej o równaniu f(x)=−⁵₃x, gdyby ta została tu uwzględniona Dziękuję Ci bardzo za pomoc

Basia: