nierówność z arctg Filip: Wykaż, że dla każdego x∊[0,∞) zachodzi nierówność: pi/2−xarctgx<1 Uwaga: rozważ osobno przypadki dla x=0 oraz x>0.

Basia: dla x=0 na pewno ta nierówność nie jest prawdziwa

π		π		π
	−0*arctg0 =		−0*0=		>1
2		2		2

a skoro nie zachodzi dla x=0∊[0;+∞) to nie może zachodzić dla każdego x z tego przedziału o ile dobrze widzę powinno być

π
	−x*arctgx > 1 dla każdego x∊[0;+∞)
2

Filip: tak dla każdego, ale mam rozważyć też dla x>0

Filip: błąd się wkradł powinno być x*(pi/2)−xarctgx<1

Basia: a to co innego

Filip: up

Filip: czy wystarczy ze oblicze wartosc w 0, nastepnie napisze ze f. jest ciagla bo jest zlozona z f. elementarnych i policze granice w +∞?

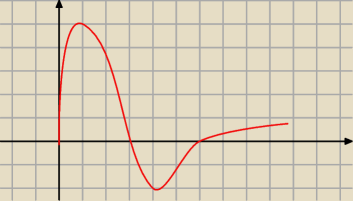
Basia: f(0)=0 f jest ciągła owszem, ale to niczego nie dowodzi może być np.tak jak na rysunku oczywiście tu tak nie jest, to tylko przykład, że ciągłość i granica w +∞ raczej niczego nie dowodzą

Basia: ale ciągłość i ekstrema mogą już coś dać

Basia:

	π
f(x) = x(		−arctg(x))
	2

	π		1
f'(x) = 1*(		−arctgx) + x*(−		)=
	2		1+x2

π		x
	−arctgx −
2		1+x2

raczej nie tędy droga