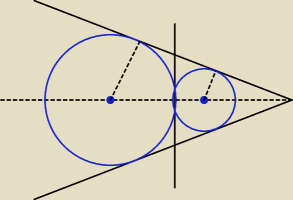
zadanie z okręgami Kalirr: Ramiona kąta ostrego o mierze 2α przecięto prostą k prostopadłą do dwusiecznej kąta, która jest odległa o d od jego wierzchołka. W ten kąt wpisano dwa okręgi, każdy styczny do obu ramion kąta i prostej k . Oblicz odległość środków tych okręgów.

g:

	r		R
sin α =		=
	d−r		d+R

	1		1		sin α
r+R = d*sin α*(		+		) = 2d*
	1+sin α		1−sin α		cos2α

Eta: r+R= 2dtgα/cosα

Eta: https://matematykaszkolna.pl/forum/153343.html Tu masz dokładny rysunek

Kalirr: Nie rozumiem tylko skąd 1−sinα i 1+sinα w mianownikach. Jak z rownania dsinα − rsinα=r wzięło się 1+sinα

Blee: Z przeksztalcenia:

	r
sinx =		⇔ dsinx − rsinx = r ⇔ dsinx = r(1+sinx) ⇔ r = ...
	d−r

Analogicznie R wyznaczasz

Kalirr: Ok już rozumiem