Wielomian z parametrem ilośc rozwiązań Marcin : Witam, proszę o pomoc w wytłumaczeniu mi jednej rzeczy. Mam zadanie " Wykaż, że dla dowolnego m e R/(0) równanie −x³ +x²(2−m²) + x(2m²+4)−8=0 ma trzy pierwiastki Dla jakiej wartości parametru m suma pierwiastków tego równania jest równa −7" Obliczyłem że dla x=2 wielomian się zeruje czyli wiem, że jest podzielny przez dwumian (x−2), podzieliłem równanie przez ten wielomian i otrzymałem trójmian kwadratowy −x²−m²x+4. Pytanie jest o wartość m dla której ten wielomian ma 3 pierwiastki Nie różne, więc delta >= 0. I teraz sedno pytania, dlaczego ten wielomian nie może mieć trzech pierwiastków =2 Czyli dlaczego muszę obliczyć że x1 nie równa się 2 i x2 nie równa się2 ? Pozdrawiam !

Janek191: − x² − m² x + 4 = 0 Δ = m⁴ − 4*(−1)*4 = m⁴ + 16 > 0 zatem ten wielomian ma dwa różne pierwiastki, czyli wielomian wyjściowy ma trzy miejsca zerowe , a równanie trzy pierwiastki. Ponadto

	m2
x1 + x2 =		= − m2 = − 9 ⇔ m2 = 9 ⇔ m = − 3 lub m =3
	−1

Suma pierwiastków − 9 + 2 = − 7 dla m = − 3 lub m = 3.

Basia: Δ=m⁴+16 dla dowolnego m Twój trójmian kwadratowy ma dwa różne pierwiastki bo dla dowolnego m Δ>0 co do reszty to kwestia interpretacji Moim zdaniem jest tak: (ale znam inne poglądy na ten temat) po pierwsze: równanie nie ma pierwiastków; równanie ma rozwiązania, pierwiastki ma wielomian po drugie: trzy rozwiązania oznacza trzy różne rozwiązania równanie (x−1)²=0 ma jedno rozwiązanie po trzecie: z pierwiastkami wielomianu jest tak samo wielomian W(x) = x²−2x+1 ma jeden pierwiastek dwukrotny

Janek191: Równanie ma pierwiastki ( rozwiązania), a wielomian ( czyli funkcja ) ma miejsca zerowe

Marcin : Dziękuje Wam bardzo. Tak jak myślałem błąd był w mojej interpretacji. Czyli pytanie o pierwiastki równania miało mnie właśnie zbić z tropu i próbować rozwiązywać to równanie jak trójmian z parametrem. Dziękuję jeszcze raz

Basia: https://pl.wikipedia.org/wiki/Wielomian#Szukanie_pierwiastk%C3%B3w to jedynie kwestia interpretacji; jak zwał tak zwał istotne jest to, że równanie x²−2x+1=0 ma jedno rozwiązanie a wielomian W(x)= x²−2x+1 ma jeden pierwiastek dwukrotny potraktowany jak funkcja, którą oczywiście jest, ma jedno miejsce zerowe

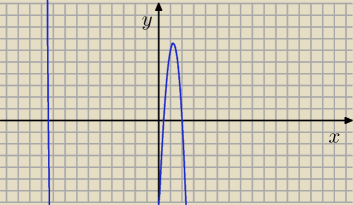
Janek191: Dla m = − 3 lub m = 3 mamy równanie: − x³ − 7 x² + 22 x − 8 = 0 lub wielomian W(x) = − x³ − 7 x² + 22 x − 8 i jego wykres.

Marcin : Dziękuje wam za takie dogłębne wytłumaczenie ! Już wszystko rozumiem