
 Bardzo ciekawe i ładne zadanko
Bardzo ciekawe i ładne zadanko  Jak zwykle w planimetrii:
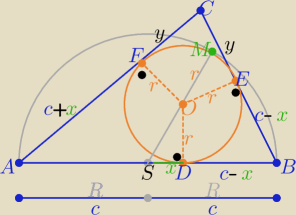
1/ przejrzysty rysunek (to połowa sukcesu) zgodnie z treścią zadania
|AB|=2R=2c ⇒ R=c i |SM|=R=c to |SO|=c−r , c>r
Z tw. Pitagorasa w ΔDOS : x2=(c−r)2−r2 ⇒ x2=c2−2rc
==========
Z twierdzenia o odcinkach stycznych :
|AD|=|AF|=c+x , |DB|= |BE|−c−x , |CF|=CE|= y
Pole trójkąta ABC możemy obliczyć z dwóch wzorów
P=rp , p −− połowa obwodu lub ze wzoru Herona
Jak zwykle w planimetrii:
1/ przejrzysty rysunek (to połowa sukcesu) zgodnie z treścią zadania
|AB|=2R=2c ⇒ R=c i |SM|=R=c to |SO|=c−r , c>r
Z tw. Pitagorasa w ΔDOS : x2=(c−r)2−r2 ⇒ x2=c2−2rc
==========
Z twierdzenia o odcinkach stycznych :
|AD|=|AF|=c+x , |DB|= |BE|−c−x , |CF|=CE|= y
Pole trójkąta ABC możemy obliczyć z dwóch wzorów
P=rp , p −− połowa obwodu lub ze wzoru Herona
| 2c+c+x+y+c−x+y | ||
p= | = 2c+y | |
| 2 |
| 2rc | ||
r(2c+y)= 2cy⇒ 2rc+ry= 2cy ⇒ y(2c−r)=2rc ⇒ y= | ||
| 2c−r |
| 2rc | ||
to P=r*(2c+y) = r(2c+ | ) =.................. | |
| 2c−r |
| 4c2r | ||
P(ABC)= | [j2] ( zależne od danych c i r) | |
| 2c−r |
 Napisz czy taką masz odpowiedź?
Napisz czy taką masz odpowiedź?