 1/ Jak pisze Krzysiek 60
1/ Jak pisze Krzysiek 60  Taki trapez jest trapezem równoramiennym
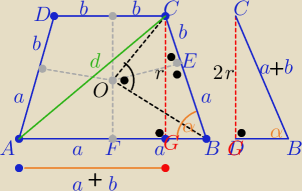
rysunek i odpowiednie oznaczenia zgodne z treścią zadania
ΔBOC jest prostokątny ( sam uzasadnij dlaczego?
to r2=ab , r −−− dł. promienia okręgu wpisanego w trapez
Okrąg opisany na trapezie jest też opisany na ΔABC
Taki trapez jest trapezem równoramiennym
rysunek i odpowiednie oznaczenia zgodne z treścią zadania
ΔBOC jest prostokątny ( sam uzasadnij dlaczego?
to r2=ab , r −−− dł. promienia okręgu wpisanego w trapez
Okrąg opisany na trapezie jest też opisany na ΔABC
| d | ||
z tw. sinusów 2R= | ||
| sinα |
| 2r | ||
W ΔGBC : (a+b)= | ||
| sinα |
| 4r2 | ||
d2=(a+b)2+(2r)2⇒ 4R2sin2α= | +4r2 | |
| sin2α |
| 4R2 | sin2α+1 | |||
to | = | |||
| 4r2 | sin4α |
| R | √sin2+1 | |||
= | ||||
| r | sin2α |
| R | a√2 | R | √1+1 | |||||
to | = | = √2 to | = | = √2 czyli ok | ||||
| r | a | r | 1 |
| 4r2 | ||
4r2+ | =4R2*sin2α ⇒ ....................... ( po przekształceniu: | |
| sin2α |
| R | √sin2α+1 | ||
= | |||
| r | sin2α |