Roznowartosciowosc funkcji
Ania: Czy funkcja jest roznowartosciowa?
f(x) =(5−3x)/(x+3)
Wytlumaczy ktoś, jak to zrobić krok po kroku?
10 lut 10:45
Krzysiek60: Mowimy ze funkcja f : X→Y (X=D
f) jest roznowartosciwowa jesli
⋀x
1 x
2 ∊X f(x
1)= f(x
2)⇒x
1=x
2
lub rownowaznie ⋀x
1 x
2 ∊D
f x
1≠x
2⇒f(x
1)≠f(x
2)
x
1. x
2 ∊R\{3}
| | 5−3x1 | | 5−3x2 | | 5−3x1 | | 5−3x2 | |
f(x1)=f(x2)= |
| +3}= |
| = |
| − |
| = 0 |
| | x1 | | x2+3 | | x1+3 | | x2+3 | |
Sprowadz to wspolnego mianownika
Wyrazenie wymierne =0 kiedy licznik =0
Z warunku x
1= x
2 ⇒x
1−x
2=0
10 lut 11:10
Ania: Już rozumiem, dziękuję😉 a jeżeli mamy funkcje f(x) =ln2x to jak mam to zrobić? Zaczęłam tak:
D=(0, ∞)
x1, x2∊D i x1≠x2
Czyli ln2x1−ln2x2=...?
10 lut 11:22
Krzysiek60: =0
Ale dalej nie wiem jak pomoc
Gdyby byly np same logarytmy to wtedy lnU{x1}[x2}=0
Tutaj musi pomoc ktos kto jest na studiach (niestety nie konczylem)
10 lut 11:35
Krzysiek60: Ma byc ≠0 bo przyjelas wersje rownowazna
10 lut 11:36
iteRacj@:
ln2 x1−ln2 x2 = ( ln x1−ln x2)*(ln x1+ln x2) i zastosuj wzory na sumę i różnicę
logarytmow
10 lut 11:48
iteRacj@:
w tym przykładzie łatwiej będzie skorzystać z wersji ⋀x1 x2 ∊D f(x1)= f(x2)⇒x1=x2
10 lut 11:54
Krzysiek60: | | x1 | |
czyli bedzie ln |
| *ln(x1*x2)=0 |
| | x2 | |
Ijak dalej ? ja tez skorzystam
| | x1 | |
Jesli x1= x2 to ln |
| =0 i razy ten drugi ln =0 ? |
| | x2 | |
10 lut 11:59
Ania: lnx1−ln2x2=(lnx1−lnx2)(lnx1+lnx2)=(ln (x1/x2)) (lnx1x2)
Pierwszy czynnik jest różny od zera, drugi też, czyli całe wyrażenie będzie różne od zera, czy
funkcja na moje jest roznowartosciowa.. Ale w odpowiedziach jest inaczej 😐
10 lut 12:08
Janek191:
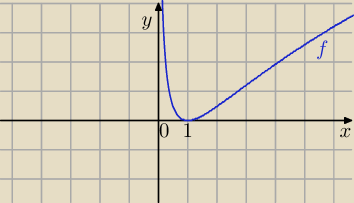
10 lut 12:11
Krzysiek60: Czyli wynika stad ze wyciagamy jakies bledne wnioski .
10 lut 12:14
Janek191:
f(x) = ln
2 x
( ln x)
2 = 1
ln x = − 1 lub ln x = 1
zatem
10 lut 12:20
iteRacj@:
sprawdzimy, czy ⋀x
1 x
2∊D f(x
1)= f(x
2) ⇒x
1=x
2
ln
2 x
1−ln
2 x
2=0
(ln x
1−ln x
2)(ln x
1+ln x
2)=0
| | x1 | |
stąd ln |
| =0 lub ln (x1x2)=0 |
| | x2 | |
czyli warunek że x
1=x
2 nie jest spełniony
funkcja nie jest różnowartościowa!
10 lut 12:37
