trapez
james: Udowodnij że odcinek łączący środki ramion trapezu jest równoległy do podstaw a jego długośc
jest równa ich średniej arytmetycznej. W tym celu podziel trapez na 2 trójkąty i NIE korzytaj
z wektorów.
Najlepiej z podobieństwa

8 lut 19:07
james: No ludzie na wszystko odpowiadacie a tu nie, pliss potrzebuję
8 lut 19:30
Basia: na trójkąty i podobieństwo nie mam pomysłu;
jak chcesz to mogę z tw.Talesa, chociaż za diabła nie rozumiem dlaczego nie z wektorów
żeby liczenie zajęło więcej czasu?
8 lut 19:40
Eta:
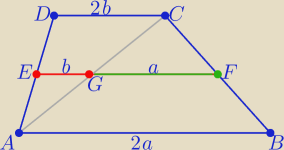
Komentarze dopisz sam.........................
......................................
8 lut 19:41
PW: Już kiedyś o tym pisałem, ale nie mogę znaleźć. Dla udowodnienia równoległości EF do AB
kluczowe jest:
1. powołanie się na twierdzenie odwrotne do twierdzenia Talesa dla obu kątów ACB i CAD (co daje
równoległość GF do AB i GE do DC)
2. powołanie się na piąty aksjomat Euklidesa, by stwierdzić, że proste GF i GE pokrywają się.
Nie jest to więc wcale łatwiutkie zadanie dla licealisty.
8 lut 20:00
Eta:

8 lut 20:02
Basia: Eta zakłada, że G jest środkiem AC, co nie jest takie oczywiste.
z tw.Talesa i odwrotnego łatwiej udowodnić nie dzieląc na trójkąty
tylko przedłużając ramiona trapezu tak by powstał trójkąt.
dość łatwo wtedy wychodzi chociaż rachunki raczej żmudne
8 lut 20:08
PW: To znaczy − ja myślę − Eta wzięła G będący środkiem AC, dlatego można stosować tw.
odwrotne do tw. Talesa.
8 lut 20:12
james: Eta ale czemu to jest rownoległe?
8 lut 20:14
james: I czmu FG=a XD
8 lut 20:15
PW: james, nie wygłupiaj się. Szkoda naszego czasu.
8 lut 20:16
Eta:
Każdy punkt leżący na środkowej jest równo odległy od końców
odcinków równoległych AB i DC
zatem G jest środkiem AC
i z tw. odwrotnego do tw. Talesa
.......................................
8 lut 20:19
Eta:
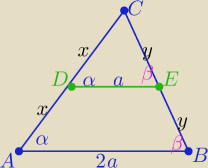
Z podobieństwa trójkątów ABC i DEC w skali k=2
|DE|= 0,5|AB|
8 lut 20:23
Mila:
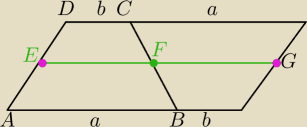
Obrót o 180
o,
|EG|=a+b
8 lut 20:27

 Komentarze dopisz sam.........................
......................................
Komentarze dopisz sam.........................
......................................

 Z podobieństwa trójkątów ABC i DEC w skali k=2
|DE|= 0,5|AB|
Z podobieństwa trójkątów ABC i DEC w skali k=2
|DE|= 0,5|AB|
 Obrót o 180o,
|EG|=a+b
Obrót o 180o,
|EG|=a+b